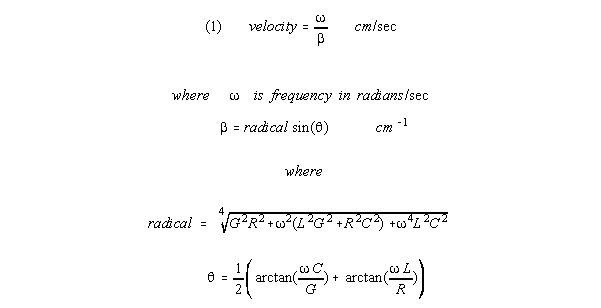
Conduction velocity - SK versus KR theory

Conduction velocity in a transmission line is a function of the effective R, L, G, C, and radian frequency of that line (hatted values under S-K theory, unhatted values under K-R theory.)     See A new passive neural equation: Part a, derivation             Equation 1 below is (13) in this reference.

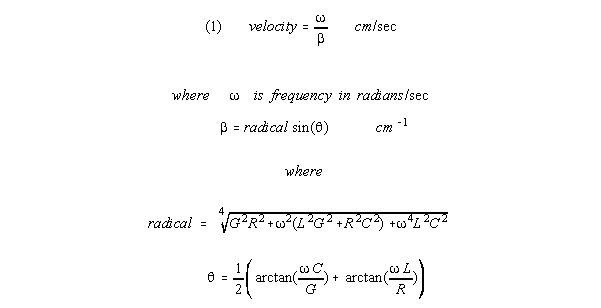
Writing (1) out, velocity is:

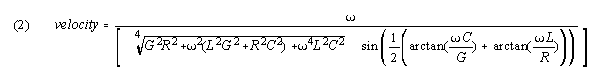
In the K-R case, L is negligible, and (2) becomes

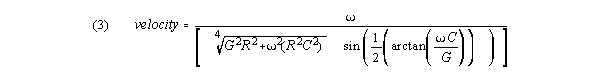
If membrane conductance, G, is set to 0, this simplifies to

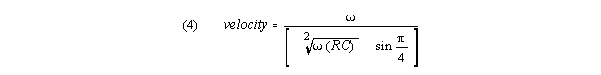
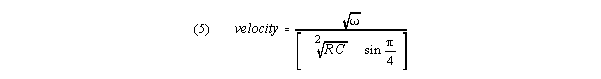
In the K-R case, with membrane conductance G set to 0, velocity is proportional to the square root of frequency. R and C are fixed for a particular line.

For the S-K case, the relevant values are the hatted values that include crossterms, and effective inductance is large, rather than negligible.

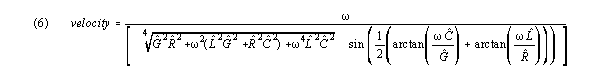
In the case where G is negligible, G hat is negligible and (6) reduces to

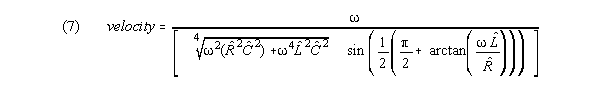
For small neural lines, the numerical value of L is much larger than R, and as frequency increases, the velocity function gets closer and closer to

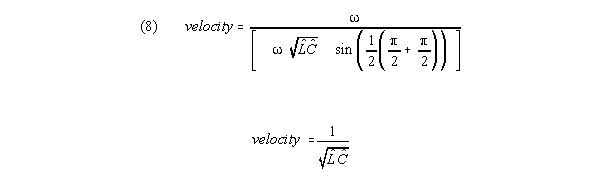
So under S-K theory, velocity for small neural lines, with G very low, is INDEPENDENT of frequency, because frequency effects in numerator and denominator cancel.

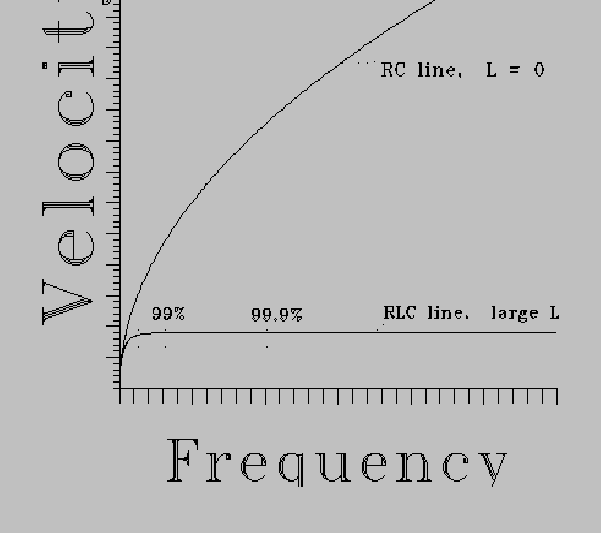
The proportional relations of velocity to frequency are shown below:. K-R calculates a line with R and C, and negligible L. S-K calculates a line with R, C, and L, with L large.      The vertical and horizontal scales are arbitrary linear scales to illustrate the shape of the curve.