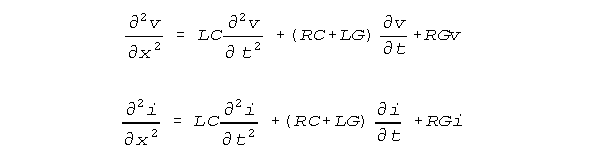
The S-K transmission equations:

The currently accepted passive neural conduction equations are the standard conduction equations of electrical engineering, usually written in a contracted form that discards the terms in L that are negligible in this equation.

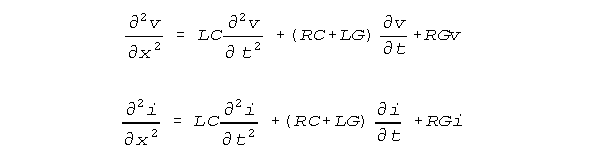
Robert Showalter and Stephen Jay Kline have found that these equations lack crossterms because special restrictions on the use of dimensional parameters in coupled finite increment equations have not been understood⁽¹¹⁾

. The crossterms, which can also be derived (within a scale constant) by standard linear algebra based circuit modelling, are negligible in most engineering applications. But these crossterms are very large in the neural context. The Showalter-Kline (S-K) equations are isomorphic to the standard conduction equations of electrical engineering and are written as follows.

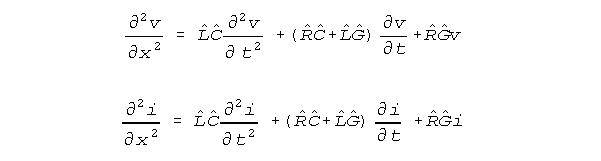
For set values of resistance R, inductance L, membrane conductance per length G, and capacitance C, these equations have the solutions long used in electrical engineering. The hatted values are based on a notation adapted to crossproduct terms. In this notation, the dimensional coefficients are divided into separate real number parts (that carry n subscripts) and dimensional unit groups, as follows.

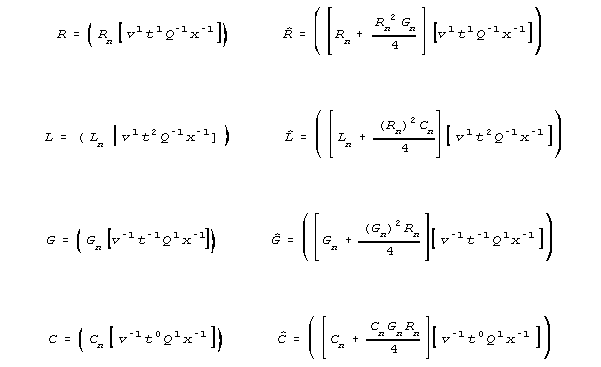
For wires,, the crossproduct terms are negligible, and the two kinds of equations are the same. But under neural conditions the crossproduct terms are LARGE. For instance, effective inductance is more than 10¹² times what we now assume it to be. The S-K equation predicts two modes of behavior.

When G is high (some channels are open) behavior similar to that of the current model is predicted.

When G is low, transmission has very low dissipation, and the system is adapted to inductive coupling effects including resonance.