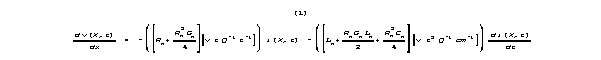
If equations derived according to Maxwell's 1st method are right, inferences from experiment are only valid over a RESTRICTED range.
Sir:
This paper offers a numerical example in support of two propositions.
The first is that our new pattern for deriving coupled equations(1)
(2) (3) from
physical models fits some evidence(4) (5).
The second is that, according to our method, some inferences from experiment
that have been generalized in an unrestricted fashion are only valid over
RESTRICTED ranges of the dimensional parametric spaces on which they are
defined.
We are taking a position that goes against "common knowledge" in mathematics and mathematical physics. We believe our formal point could be easily taught to fresh students. Our point fits evidence. But our point is psychologically hard for people of established experiences and habits of thought, however able they may be(6)
. All of us make assumptions in our patterns of thought. The more well
trained and automatic our thought patterns become, the harder it is to
question (or even identify) our assumptions(7).
Most scientists would be quick to agree to the following admonition by
George Johnson(8), taken as an expression
of an ideal:
"
Scientists must constantly remind themselves that the map is
not the territory, that the models
might not be capturing the essence of the problem, and that the
assumptions built into
a simulation might be wrong.(9) "
Even so, most scientists would make exceptions, including some unconscious
exceptions(10), and would elevate some
"universally acknowledged" ideas and patterns to the status of
unquestionable articles of faith, no longer subject to reconsideration.
For instance, our basic mapping patterns at the interface between measurable
physics and mathematical representation seem beyond doubt. Who can imagine,
after so much work and experience, that these usages could be wrong? One
might as well question arithmetic. Even so, we have found that the mapping
usages between physical map and analytical territory do contain a mistake,
and in particular an error in the usage of arithmetic. A rule restricting
arithmetic with dimensional parameters has not been understood. As a consequence,
invalid arithmetic has sometimes been accepted, and has sometimes misled
us.
We have faced the following strongly felt but false inference repeatedly:
"If the procedural change that Showalter
and Kline suggest is right, wouldn't it invalidate many results that everyone
has good reason to trust?"
The question is reasonable. An affirmative answer seems self-evident
to many. Nonetheless, the answer is no. The error that we have found can
be important (under conditions where our current models do not work well)
and yet seems totally insignificant in the cases where our models already
work well.
This paper offers an example, the conduction equation. We've derived
a new conduction equation, with new terms. In the cases where the old derivation
works well empirically, the new procedure works just as well. The new terms
are too small to matter. In the case of neural function, where the old
derivation fails, the new derivation has the properties needed to describe
behavior. The same equation, with the same terms, has enormously different
properties depending on what the numerical values of the dimensional parameters
in it happen to be.
We have shown that differential equations derived from coupled physical models may have crossterms, now thought to be infinitesimal, that are finite(11). The transmission line equations, derived elsewhere(12), are scientifically interesting examples. A partial expansion of one of these equations follows:
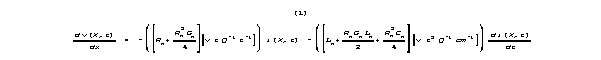
![]()
![]()
R is resistance per length, L is inductance per length,
G is membrane conductance per length, and C is capacitance
per length.
For many values of R-L-G-C, all the terms
in (1) that include products of R, L, G, and
C will be very small. However, some of these crossproduct terms
can be enormous for different values of R, L, G, and
C. Comparison of a wire case and a neural dendrite case shows the
contrast in values that can occur.
For a 1 mm copper wire with ordinary insulation and placement, typical values of the dimensional parameters would be:
R = .14 x 10-2 ohm/m C = 3.14 x 10-7 farads/m
G = 3.14 x 10-8 mho/m L = 5 x 10-7 henries/m
Here is (1) with the numerical value of terms set out below the symbolic expression of the terms:
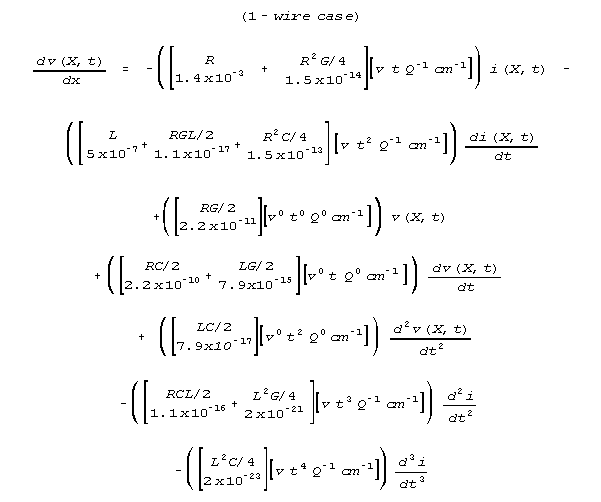
Here are the corresponding dimensional parameter values for a 1 micron
diameter neural dendrite, assuming accepted values of axolemma conductivity,
capacitance per membrane area, and inductance per unit length (volume conductivity
110 ohm-cm g = 3.18 x 10-5 mho/cm2 c=10-6
farads/cm2.)
R = 1.4 x 1012 ohm/m L = 5 x 10-7 henries/m
C
= 3.14 x 10-8 farads/m G
= 3.14 x 10-6 mho/m
Note that R is 1011 larger than in the previous case
of the wire.
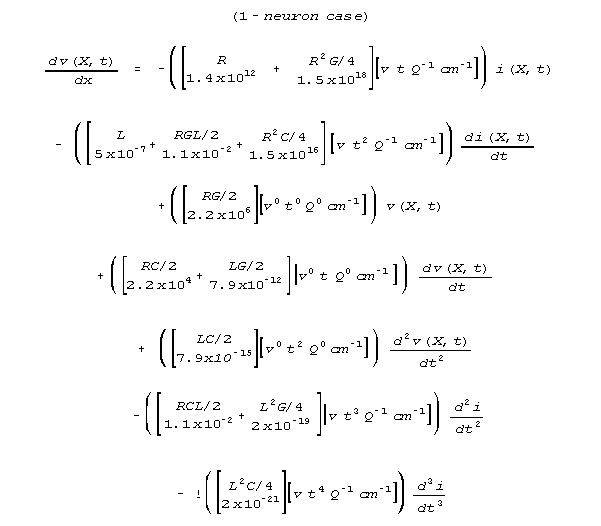
Crossproduct terms that were trivial in the wire case
become dominant in the neural dendrite case.
For the wire case, the numerical values of the primary terms (the numerical
values of the dimensional parameters R, L, G, and
C) are compared with the numerical values of the numerically most
important crossproduct terms in the voltage gradient transmission equation
below.
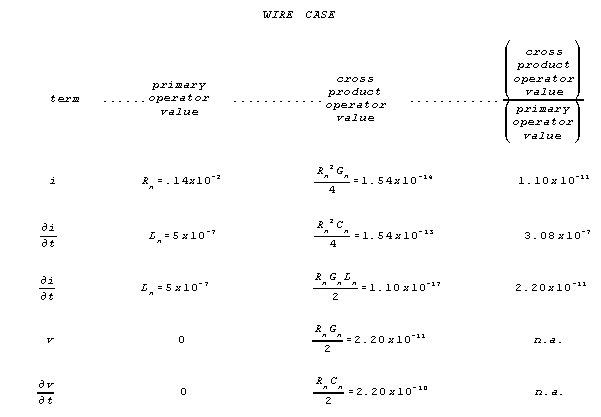
None of the crossproduct terms are big enough to attend to in a practical
model equation. The sensible formula to use for this particular set of
values of R, L, G, and C is the one Lord Kelvin
derived in 1855:
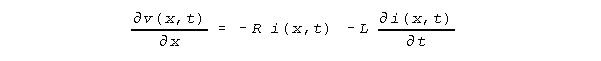
In the wire case the crossproduct terms are finite, but operationally
negligible, and undetectably small.
For the neural dendrite, some of these crossterms become dominant terms. The numerical values of the primary terms (the numerical values of the dimensional parameters R, L, G, and C) are compared with the numerical values of the numerically most important crossproduct terms in the voltage gradient transmission equation below.
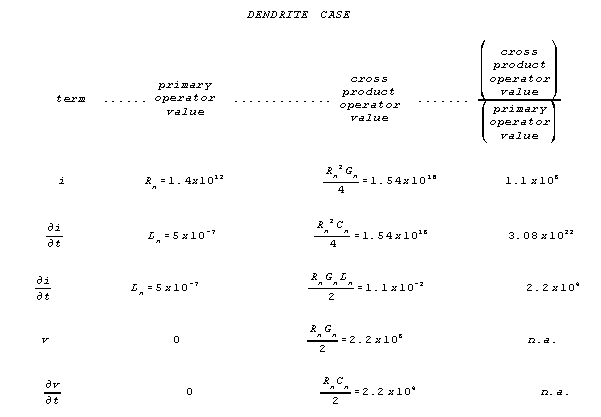
For these neural values of R, L, G, and C,
two crossproduct terms that were too small to attend to in the wire case
have become dominant terms. Magnetic inductance, L, has become too
small to include, because for these values of R, L, G, and C, the R2C
crossproduct term is 3 x 1018 times bigger than the first order
L.
Current neurological modelling of dendrites uses the same equation that
models the wire. This radically understates effective inductance.
Sensible modelling formula for the dendrite involves the following quite
different choice of terms. (Note that this equation is a selection of important
terms among others; it is an approximation that approximates reality well
enough in a particular regime of R-L-G-C.)
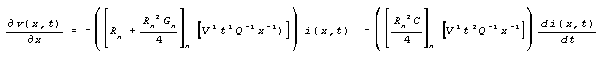
The effective inductance is 1016 times larger than in the
Kelvin (or Kelvin-Rall) equation. would be
Lines that have been thought devoid of inductance,
and incapable of inductive effects such as resonance, have very large effective
inductance.
The notion that solutions are parameter
dependent is well established in some fields, for example viscous fluid
flow. That notion applies to these new terms. In the neural transmission
case and elsewhere, crossterms now dismissed as infinitesimal are finite,
and can be large. Electrical measurements testing the conduction
equations have been carefully and accurately done, over a limited range
of parametric values. They have been "experimentally perfect"
over that range. Nevertheless, too large an extrapolation beyond that tested
range of parametric values can be treacherous. Because the dimensional
parameters that we use in our physical representations operate with type-restricted
arithmetic rules, terms we have thought to be zeros are finite. We must
take this into account when we extrapolate an equation that may be "a
perfect match to experiments" in one range of parameters into some
very different range of parameters.
M. Robert Showalter
Madison, Wi. USA
Stephen Jay Kline
Stanford, Ca. USA
NOTES:
1. Showalter, M.R., and Kline, S.J. A (1997) MODELLING OF PHYSICAL SYSTEMS ACCORDING TO MAXWELL'S FIRST METHOD
2. Showalter, M.R., and Kline, S.J. B (1997) COUPLED PHYSICAL FINITE MODELS INVOLVE DIMENSIONAL PARAMETERS AND MUST BE SIMPLIFIED IN INTENSIVE FORM
3. Showalter, M.R. A (1997) A new passive neural equation. Part a: derivation.
4. Showalter, M.R., and Kline, S.J. C (1997) Equations derived by Maxwell's first method restrict the range of applicability of inferences from experiments.
5. Showalter, M.R. B (1997) HYPOTHESIS: DENDRITES, DENDRITIC SPINES, AND STEREOCILIA HAVE RESONANT MODES UNDER S-K THEORY
6. Mill, J.S. (1869) THE SUBJECTION OF WOMEN
from HISTORY OF IDEAS ON WOMAN, R. Agonito, ed. Putnam, 1977.
Here are interesting excerpts, that still seem fresh today, that do not
establish the rightness of any particular questioning of "common knowledge,"
but that do set out difficulties that go along with that questioning:
" In every respect the burden is hard on those who attack an almost
universal opinion. They must be very fortunate as well as unusually capable
if they obtain a hearing at all. They have more difficulty in obtaining
a trial, than any other litigants have in obtaining a verdict. If they
do extort a hearing, they are subjected to a set of logical requirements
totally different from those exacted from other people." . .
" The difficulty . . . exists in all cases in which there is a
mass of feeling to be contended against. So long as an opinion is strongly
rooted in the feelings, it gains rather than loses in stability by having
a . . . weight of argument against it. For if it were accepted as the result
of argument, the refutation of the argument might shake the solidity of
the conviction; but when it rests . . . on feeling, the worse it fares
in argumentative contest, the more persuaded its adherents are that their
feeling must have some deeper ground, which the arguments do not reach;
and while the feeling remains, it is always throwing up fresh entrenchments
of argument to repair any breach made in the old.
". . . a cause supported on the one hand by universal usage, and
on the other hand by so great a preponderance of popular sentiment, is
supposed to have presumption in its favour, superior to any conviction
which any appeal to reason has power to produce in any intellects but those
of a high class.
" I do not mention these difficulties to complain of them, first,
because it would be useless; they are inseparable from having to contend
with people's understandings against the hostilities of their feelings
and practical tendencies: and truly the understandings of the majority
of mankind would need to be much better cultivated than has ever yet been
the case, before they can be asked to place such reliance in their own
power of estimating arguments, as to give up practical principles in which
they have been born and bred and which are the basis of much of the existing
order of the world, at the first argumentative attack which they are not
capable of logically resisting. I do not quarrel with them for having little
faith in argument, but for having too much faith in custom and the general
feeling."
7. Kuhn, T.S. (1962) The Structure of Scientific Revolutions U.of Chicago Press, Chicago Chapter 6.
8. See http://www.santafe.edu/~johnson and Science Forums for THE NEW YORK TIMES at http://www.nytimes.com/.
9. Johnson, G. (1997) Proteins Outthink Computers in Giving Shape to Life NEW SCIENTIST March 25 1997.
10. Johnson, G. (1996) FIRE IN THE MIND: Science, Faith, and the Search for Order Vintage, N.Y. p. 200.