
EQUATIONS FROM COUPLED FINITE INCREMENT PHYSICAL MODELS MUST BE SIMPLIFIED IN POINT FORM.
M. Robert Showalter(1) and Stephen J.
Kline(2)
When we derive a differential equation (defined at a point) from
a coupled finite increment physical model, we must put ALL the variables
and increments in our model equation into POINT FORM prior to algebraic
simplification. The point forms of spatial quantities and time (in cm and
second units) are:
length at a point: (1 cm)p area at a point: (1 cm2)p
volume at a point: (1 cm3)p a
point in time: (1 second)p
with UNITS of length, area, volume, and time
and
NUMERICAL VALUES of 1 = length/length, 1= area/area
1
= volume/volume, and 1=
time/time respectively
We rederive the neural transmission equation using the point form
of length, and find new terms. Some of these terms are enormous and dominant
terms in the regime of neural function, and have important medical implications.
MATHEMATICAL BACKGROUND:
For reasons cited elsewhere(3), particularly
Regan's data(4), we concluded that neural
lines must conduct according to a law different from Kelvin-Rall (K-R)

with effective inductances ten or more orders of magnitude larger than
K-R showed. We concluded that there had to be nonlinear terms, strongly
dependent on diameter, that had been wrongly discarded. We quickly found
terms in the derivation that appeared to be the right size and of the right
form (on one interpretation). But these terms (on the conventional interpretation)
were discarded as "infinitessimal." After a long process of elimination,
we set out to question conventional limiting arguments used in physical
mappings, not because we had substitute arguments in hand, but because
we felt our evidence forced us to do so. We were not questioning formal
mathematics in the axiomatic domain of the algebra. We were questioning
procedures, that no one was really clear about, that mapped from physically
measurable systems into the domain of the algebra. We were doing
classical physics on a classical problem.
By far the hardest part of this investigation, for us and for people
who have looked at our work, has been the idea that there COULD be a mistake
in our procedures for going from measurable physical models to formal (axiomatic
and abstract) models. From the start, we agreed with George Johnson's(5)
admonition that:
" Scientists must constantly remind themselves that the map
is not the territory, that the models might not be capturing
the essence of the problem, and that the assumptions built
into a simulation might be wrong.(6)
"
But for us and for others, established mapping patterns at the interface
between measurable physics and mathematical representation seemed beyond
doubt. It was difficult to question these patterns at all. Only after much
time did it become clear to us that these usages, themselves, had to contain
an error. Only after much more time did it occur to us that the error was
at the level of arithmetic. Even so, we have found that our mapping usages
between physical territory and analytical map do contain a mistake, and
in particular an error in the usage of arithmetic. A rule restricting arithmetic
with dimensional parameters has not been understood. As a consequence,
invalid arithmetic has sometimes been accepted, and has sometimes misled
us. No one with long experience and built-up reflexes of thought committed
to the established mapping procedures can be asked to enjoy our conclusions.
We can ask that they be evaluated on the basis of reason and evidence,
even against the inclinations of reflex and emotion. We've found these
conclusions difficult, too. At the same time, we believe that these conclusions,
applied in neural science and medicine, will improve some lives, and save
some lives. We also believe that these conclusions may facilitate other
technical work.
We've had to reexamine derivational foundations that had worried J.C.
Maxwell(7) (8).
Can derivations be done using symbols that stand explicitly for the
detailed physical quantities they represent, or is it necessary to abstract
these symbols to numbers so that calculation can go on? We found that to
answer this question, we needed a clearer understanding of the symbol constructs
that we logically must use to represent "detailed physical quantities."
We've found that there must be a physical, context-connected modelling
domain that differs from the context-free domain of the algebra, that
uses these symbol constructs. We've had to define the dimensional parameters,
entities, long used without clear definition, that do not exist in the
domain of the algebra. We then found that the dimensional parameters were
subject to a special type restriction on multiplication and division, explained
below, that did not correspond to anything in the domain of the algebra.
Derivations of coupled physical models without knowledge of this type restriction
can produce false infinitesimals, and sometimes false infinities. With
the dimensional parameters defined and properly used, derivations CAN be
done using symbols that are explicit representations of the detailed physical
quantities they represent. These derivations can be converted, without
misrepresentation, into abstract equations.
The dimensional parameters are the entities that interface between our experimental inferences and the formalities of abstract, symbolic mathematics. Our natural laws are not derived from axioms. They are logical inferences based on experiments.
All dimensional numbers, including the dimensional parameters, can be expressed in an explicit form as follows(9) (10):
![]()
Pn is a real number. The Xi's are
dimensions that may be abstract dimensions, or that may be measurable dimensions
such as length, charge, voltage, etc. The Xi's are raised
to dimensional exponents. The value of Pn that represents
a particular physical quantity depends on the units in which the
dimensions are expressed(11) (12)
(13). Units are conventional standards
(such as those of the MKS or CGS system,) that measure dimensions or quantities
expressed in terms of groups of dimensions.
The dimensional parameters are usually taken for granted, but we have found it necessary to point them out and define them. Here is an example of a dimensional parameter in use. The inductance, L, of a particular wire is the dimensional and numerical constant that expresses the physical relation between the gradient of voltage as a function of position, time and the derivative of current as a function of position and time. The inductance per unit length of a wire can be written
![]()
where v is volts, t is seconds, Q is coulombs, and x is cm. In the usual compact form, the units are implicit. We may write the natural law of inductance on the wire as follows:

We may set out this same relation with the numerical and dimensional
parts explicitly written as dimensional numbers.

The numerical parts multiply, and the dimensional parts multiply in
the sense of addition of exponents. Note that (4) and (5)
are differential equations, defined at points even though both dv/dx
and L include measurement notions set out per unit length.
The unfamiliar notion of "length at a point" is inherent.
Here are some directly measurable dimensional parameters (often referred
to as properties):
mass, density, viscosity, bulk modulus, thermal conductivity, thermal
diffusivity, resistance (lumped), resistance (per unit length), inductance
(lumped), inductance (per unit length), membrane current leakage (per length),
capacitance (lumped), capacitance (per unit length), magnetic susceptibility,
emittance, ionization potential, reluctance, resistivity, coefficient of
restitution, and many more.
In addition to the directly measurable dimensional parameters and
dimensional parametric functions there are also compound dimensional parameters,
made up of the products or ratios of dimensional parameters and other dimensional
variables. A famous class of the compound dimensional parameters is
the dimensionless numbers, such as the Reynolds number(14).
DEFINITION: A dimensional parameter
is a "dimensional transform ratio number" that relates two measurable
functions numerically and dimensionally. The dimensional parameter is defined
by measurements (or "hypothetical measurements") of two related
measurable functions A and B. The dimensional parameter is the algebraically
simplified expression of {A/B} as defined in A = {{A/B}} B. The dimensional
parameter is a transform relation from one dimensional system to another.
The dimensional parameter is also a numerical constant of proportionality
between A and B (a parameter of the system.) The dimensional parameter
is valid within specific domains of definition of A and B that are operationally
defined by measurement procedures.
Example: A resistance per unit length determined for a specific wire
for ONE specific length increment and ONE specific current works for an
INFINITE SET of other length increments and currents on that wire (holding
temperature the same.)
For example, for a length x along the wire, the voltage difference is set out
![]()
for this case, voltage drop is proportional to length between points
of reference, x times (average) current over the interval.
The dimensional parameters are not axiomatic constructs. They
are context-based linear constructs that encode experimental information.
We've implicitly assumed that
"dimensional parameters are just dimensional
numbers."
without any mathematical justification at all. This assumption
makes the difference between the "first method" to the "second
method" of Maxwell(15) (16).
For instance, derivations of a wire or line conduction model from a
finite physical model yields equations(17)
such as the following, which have many terms that would be rejected out
of hand as "infinitesimal." For example, equation (7),
![]()


which may be "simplified" according to common arguments to
(8)



Commonly, terms like those below the first line in (7
or 8) are dismissed out of hand as infinitesimal.
Difficulties with this dismissal on the basis
of meaning have been set out elsewhere(18).
Even setting these meaning issues aside, the dismissal fails several numerical
closure tests. At a finite scale, before taking the limit, the terms below
the first line are supposed to represent finite quantities. Yet when we
take the limit as x goes to zero, these crossterms are infinitesimal,
and are discarded in the differential equation. Now, let's take that differential
equation, and integrate it back up to specific scale x. We get an
equation that lacks the crossterms that we know existed at scale x
in the first place. This is not closure. The derivation is inconsistent
with itself, and the disparity can be numerically large.
The expressions in curly brackets in (7 and 8) also fail a conservation test that representations of physical circumstance must pass. Consider a curly bracketed expression in x2. If x is divided into ten pieces, and those ten subintervals are computed and summed, that sum is only 1/10 the value for the same expression computed over interval x, taken in one step. We can make the "physical" value on the interval x vary widely, depending on how many subintervals we choose to divide x into. This is not physical behavior.
These expressions are also numerically meaningless because they are
constructed on the basis of a type invalid arithmetic, as shown below.
A "number" or "expression" that can be manipulated
by "proper arithmetic" and permissible unit changes so that it
has any value at all is meaningless. Let's look at a simple loop test,
analogous to many closure tests in physical logic. In Fig. 1, an
algebraically unsimplified dimensional group that includes products or
ratios of dimensional numbers, such as one of those in curly brackets in
(7) or (8), is set out in cm length units at A. This
quantity is algebraically simplified directly in cm units to produce "expression
1," dealing with the dimensional parameters and increments as
"just numbers." The same physical quantity is also translated
from A into a "per meter" basis at C. The translated
quantity at C is then algebraically simplified to D in the
same conventional fashion. The expression at D, expressed in meter
length units, is converted to a "per cm" basis to produce "expression
2." Expression 1 and Expression 2 must be the same, or the
calculation is not consistent with itself. Quantities like those in
the curly brackets consistently fail the loop test. By choice of unit changes,
and enough changes, such "quantities" can be made to have any
numerical value at all. Expressions such as those in curly brackets in
(7) or (8) are meaningless as usually interpreted.
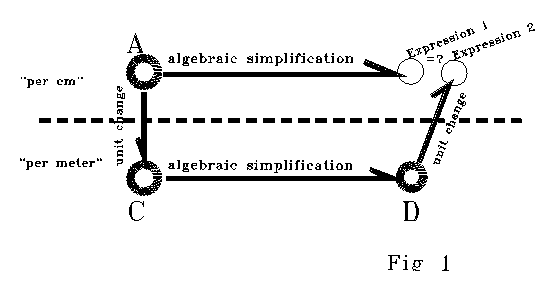


The loop test fails!
The loop test fails because a standard procedure is flawed.
Before algebraic simplification, going from one unit system
to another adjusts not just the numerical value of dimensional properties
in the different unit systems, but numerical values corresponding to the
spatial variable (length), as well.
After algebraic simplification, one has a compound dimensional
property - adjusting it to a new unit system corresponds to adjusting numerical
values that correspond to the unit change for the dimensional properties
only, with no corresponding adjustment for the absorbed spatial variable.
The result is an irreversible, numerically
absurd, but now standard mathematical operation. The difficulty has been
deeply buried and hidden in our notation.
Note that the loop test of Fig. 1 only
fails for terms that are now routinely discarded as "infinitesimal"
or "infinite" without detailed examination. Multiplication
and division of groups of dimensional numbers (and dimensional parameters)
without spatial or temporal increments works without difficulty, with numerical
values handled arithmetically, and dimensional exponents added and subtracted
in the usual way. Dimensional parameters associated with increments according
to the exact pattern that defined the dimensional parameters also work.
Problems arise when we associate several dimensional parameters together
with several increments, where the increments correspond to different physical
effects evaluated over the same interval. The procedure we have used for
evaluating such circumstances involves a kind of multiple counting that
yields perverse results, as the loop test shows. We want to incorporate
a rule that avoids mistakes like this. The rule needed restricts multiplication
and division of dimensional parameters and increments to point form. It
requires us to clarify our concept of increments (of length, area, volume,
or time) defined at a point.
Notated as we have notated them, and interpreted as we have interpreted
them, entities that represent coupled relations are physically unclear
and numerically undefined. Although we may notate the interaction of resistance,
capacitance, and resistance together in interaction with the measurable
di/dt over the interval x as

where x is a number times a length unit, the loop test shows
that this notation, literally interpreted, does not correspond to any consistent
numerical value when unit systems are changed, and then changed back.
Let's rewrite (9) setting out a notation that makes explicit
problems we need to solve concerning our notation of "length at a
point" in this expression:

That is, we are trying to express "length" at a point (the
asymptotic notion that a "differentially small" length reflects.)
R and C are already in point form, both numerically and dimensionally.
di/dt is defined at a point. If we had an point form for length,
there would be no reason for a limiting argument in (9) or (10).
Let's think of what we already do when we reason from measurement. Our
measurement procedures define things in terms of spatial variables (length,
area, volume, time) and other dimensions (voltage, charge, and many others).
The measurements are inherently finite in nature. Still, we speak of properties
in POINT FORM, defined at points. (For instance, we speak of "resistance
per unit length defined at a point" even though a point has 0 length.
The numerical-scaling argument we use to arrive at point properties is
simple and nearly reflexive. To intensify our properties, we say
that
"the property at a point is the property that we get from a
logic of interpolation from a finite scale to finer and finer scales. The
interpolation assumes homogeneity of the model down to a vanishing spatial
(and/or temporal) scale."
For example, consider the notion of resistance per unit length. Let's idealize the wire as a line. The resistance R expresses voltage gradient per unit length, per unit current. For any interval that includes length, the basic notion of resistance can be directly defined "per unit length". Other properties can be defined in similar ways "per unit area" or "per unit length" over finite areas, or finite volumes. But the notion of "length (or area, or volume) at a point" is an abstraction. This extremely useful and inescapable abstraction is much older(19)
than some of our rigorous calculus formality(20).
In thermodynamics and elsewhere, we don't intensify our extensive variables
by a calculus argument of any kind. We just assume that the property we're
considering is homogeneous, and write our point form variables directly.
The abstract notion of length or area or volume "at a point"
is already embedded in many of the point form properties in common use.
Using cm and second units, the point forms of the properties of length,
area, volume and time are:
Point form of length = { 1 length/length (length unit)}
length at a point in cm units: ( 1 cm )p
Point form of area = { 1 area/area ( (length unit)2 ) }
area at a point in cm units: ( 1 cm2 )p
Point form of volume = { 1 volume/volume ( (length unit)3) }
volume at a point in cm units: ( 1 cm3 )p
A point in time:
{ 1 (time increment)/(time increment) ( (time unit) ) }
a point in time in second time units: ( 1 second )p
The subscript is a marker, without arithmetic significance, that
may be read as "at a point." The dimensions of length, area,
and volume are length to the first, second and third power respectively.
The numerical coefficients are identity operators, 1, because, for even
the smallest imaginable numerical values of length, l, area, a;
or volume v
l/l = 1 a/a = 1 v/v = 1
and t/t = 1
We can rewrite (10) as

Substituting the point form of length into (7) or (8)
in place of x, we may algebraically simplify the bracketed expressions
in the equation(s). This separates R, L, G and C
into numerical parts (Rn, Ln, Cn,
and Gn) that are algebraically simplified together, and
unit groups that are algebraically simplified together (by adding exponents.)
We'll choose a semi-arbitrary voltage-unit, charge-unit, cm, time-unit
system here (v-Q-cm-t units.) We get:

![]()
![]()
The analogous di/dx equation is

![]()
![]()
Each term consists of one (compound) dimensional parameter times
a measurable. These differential equations, when integrated to length x,
reconstruct the values that apply to that length x, with no lost
terms. Every term in these differential equations passes the loop test
of Fig 1. We may map these differential equations symbol-for-symbol
into corresponding partial differential equations. We may map these differential
(or corresponding partial differential) equations symbol-for-symbol into
the domain of the algebra. These equations are different equations from
the Kelvin-Rall equations (1) now used in neurophysiology.
An important difference is the effective inductance term. For
unmyelinated axons and dendrites in the neural range of sizes, the numerical
magnitude of R2C/4 is between 1012 and 1021
times larger than L, depending on dendrite diameter and other variables.
This term, which is much too small to measure in large scale electrical
engineering(21), is a dominant and practically
important term at neural scales in neural tissue.
Many terms now thought to be "infinities" are also finite
terms when they are correctly interpreted in point form.
We have shown that physical domains, that include dimensional parameters
that represent measurable circumstances, differ from the domain of the
algebra. Unless we know this, we can discard important terms, and delude
ourselves, or form false infinities, and delude ourselves. We can avoid
this if we follow the following lesson:
OPERATIONAL LESSON:
When we represent a finite increment physical system in the form
of a differential equation (defined at a point) we must put ALL the variables
and increments into POINT FORM - it is not valid to have all the quantities
except the increments in point form, with the increments in extensive form.
The point forms of spatial quantities and time (expressed here in cm and
second units) are:
length at a point: (1 cm)p area at a point: (1 cm2)p
volume at a point: (1 cm3)p a
point in time: (1 second)p
with UNITS of length, area, volume, and time
and
NUMERICAL VALUES of 1 = length/length, 1= area/area
1 = volume/volume, and 1=
time/time respectively
With ALL the variables and increments in our equation representation
set out in point form, algebraic simplification yields a differential equation
that validly represents our system.
Notes:
1. Department of Curriculum and Instruction, School of Education, University of Wisconsin, Madison, USA.
email: showalte@macc.wisc.edu
2. Department of Mechanical Engineering, Stanford University, Stanford Ca. USA.
3. Showalter, M.R. A (1997) Reasons to doubt the current neural conduction model. available FTP angus.macc.wisc.edu/pub2/showalt
4. David Regan (1989) HUMAN BRAIN ELECTROPHYSIOLOGY: Evoked Potentials and Evoked Magnetic Fields in Science and Medicine Elsevior pp. 106-108.
5. See http://www.santafe.edu/~johnson and Science Forums for THE NEW YORK TIMES at http://www.nytimes.com/.
6. Johnson, G. (1997) Proteins Outthink Computers in Giving Shape to Life NEW SCIENTIST March 27, 1997.
7. Maxwell, J.C. (1878) DIMENSIONS ENCYCLOPEDIA BRITANNICA, 9th ed.
8. Showalter, M.R., Kline, S.J. A (1997) Modelling of physical systems according to Maxwell's first method. available FTP angus.macc.wisc.edu\pub2\showalt
10. 8. Kline, S.J. (1965, 1984) Similitude and Approximation Theory, McGraw-Hill; Springer-Verlag, Chapter 2.
12. 10. Kline op. cit. Chapter 2.
13. 11. Bridgman, P.W. (1922, 1931) Dimensional Analysis Yale University Press, New Haven, Chapters 2, 3.
14. Kline, op. cit. Chapter 3. See tables 3.1, 3.2.
17. Showalter, M.R. B (1997) A new passive neural equation. Part a: derivation. available FTP angus.macc.wisc.edu\pub2\showalt
19. In PRINCIPIA MATHEMATICA (1687) Book 2, following prop XL, Isaac Newton discusses the propagation of sound. He employs two numbers that moderns would call "dimensional parameters" in his treatment. The first is mass of air per unit volume at a point. The second is compressibility of air per unit volume at a point. These dimensional entities are only experimentally definable in finite terms, but they are set out in intensive (point) form. Numerically and dimensionally, the intensive and extensive form of these numbers is the same.
20. 18. Compare Newton in the 1680's versus the work of Weierstrass and his school in the 1870's, set out in H. Poincare L'oeuvre mathematique de Weierstrass" Acta Mathematica, XXII, 1989-1899, pp 1-18.
21. Showalter, M.R. and Kline, S.J. B (1997) If equations derived according to Maxwell's 1st method are right, inferences from experiment are only valid over a RESTRICTED range.
available FTP angus.macc.wisc.edu\pub2\showalt