PROPOSED SYSTEMS OF NEURAL NETWORKS FOR POLYNOMIAL PROCESSING

M. Robert Showalter
University of Wisconsin, Madison

       Monolateral inhibitory or excitatory arrays, if tightly calibrated, are mathematically powerful structures.    It is suggested that these arrays could pack a surprising amount of mathematical power into a compact mass of neural tissue.    The arrays shown here, working in combination with some switching elements, can solve polynomial equation systems.    The arrays and patterns set out here are simple, and should be of widespread biological interest, either as direct models of nerve tissue or as analogs to biological function.   The arrays are fast.   Most of the computation in these networks is massively parallel.   With the neurons in the arrays working at ordinary neuron speeds, these array systems should be able to execute complex calculations as quickly as animals actually do them.   The arrays shown here are adapted to the encoding of polynomials into efficient codes.   Matched and inverse arrays are adapted to convert codes back to patterns.   These matched arrays, along with some supporting arrays, make possible a broad class of geometrically, logically, and linguistically oriented neural code systems.   The arrays are particularly adapted for rapid recognition and manipulation of faces or other image forms.

     Neurons, glia, and synapses outnumber genes by factors of millions, tens of millions, and billions respectively in humans and other higher vertebrates.   It follows that explanation of neural systems in higher vertebrates must involve more than cell biology, molecular biology, and the study of preparations consisting of a few cells.   Development of organized neural structures must also involve self organization onto mathematical-geometrical patterns which are robust and of a high-enough intrinsic probability.

     This paper proposes a candidate structure and system of structures which combine high intrinsic probability with surprisingly great computational power.   The base structure is a refinement of lateral inhibition or lateral excitation arrays that have long been known in brains. This structure manipulates polynomials.   Coordinate structures are also proposed that may have evolved in a long sequence of relatively short, sensible steps.   Detailed discussion of the mathematical and hypothetically biological structures is set out here, and includes emergent substructures of biological plausibility.

     The networks here relate directly to the many examples of lateral inhibition known to biology.

         The notion of lateral inhibition is well established. Laughton⁽¹⁾ summarized a mass of neurological knowledge as follows:

" During sensory processing one component of the stimulus is often subtracted from another. Such antagonistic interactions play a number of roles, as illustrated by lateral inhibition. In the visual system, lateral inhibition enhances the responses to intensity fluctuations by, as Ernst Mach put it, "effacing the mean." Lateral interaction also generates useful spatial filters in the mammalian visual system (e.g., KOCH, WANG & MATHUR) and sharpens localization in the Mormyromast system of gymnotid electric fish (BELL). When sound frequency is mapped by lineal position, inhibition sharpens spatial tuning by suppressing responses to side bands (SUGA). The receptive fields of interneurones coding mechanosensory inputs from the locust leg exhibit pronounced inhibition that removes the unchanging signal component (BURROWS). In the fly retina, antagonism removes the unchanging signal component (LAUGHTON) associated with the mean light level. The elimination of this standing signal reduces the risk of saturation and maintains signal operations in the region of highest gain. ...


Here, Laughton goes on to a statement, much like many other statements in the literature, that I wish to refocus:


"This observation helps explain why a fine balance between inhibitory and excitatory components is a property of so many sensory neurones and processes."


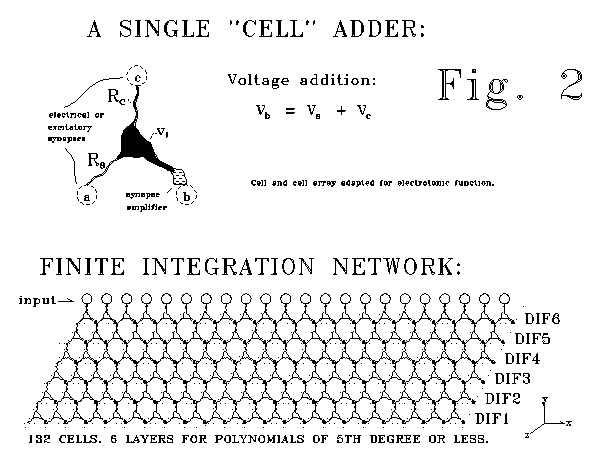
I suggest that a system characterized by lateral inhibition could be a tightly calibrated finite differencing array.   Figure 2 illustrates such an array.   Such an array system would probably be matched or linked to an inverse array system, an asymmetric lateral excitation array such as that shown in Figure 1.   The arrays of Fig. 1 and Fig. 2 would respond to experimental interrogation in ways that could be roughly described as "inhibition" and "excitation."    However, the phrase "a fine balance between inhibitory and excitatory components" would be inadequately clear unless the notions of inhibition and excitation were used quantitatively on a cell-by-cell basis, and used in the context of specific geometry.   Sharpening these notions in this quantitative and geometrical way seems justified.   The arrays of Fig. 1 and Fig. 2 are "simply" tightly calibrated and monolateral (rather than bilateral) inhibitory or excitatory arrays.   Such forms have been discussed for nearly a century.   However, these arrays could pack a surprising amount of mathematical power into a compact mass of neural tissue.  These arrays can manipulate polynomials.

1. INTRODUCTION AND MATHEMATICAL-HISTORICAL CONTEXT

       Polynomials are basic.    People operating at the conscious, cultural level compute or define most functions above arithmetic by means of polynomials or infinite polynomial series. The existence of polynomial-manipulating systems in animals has long seemed likely.   From an engineering perspective, it is hard to think about the performance of a bat, a bird, a baseball player, a ballerina, or a car-driving academic without concluding that these beings solve complicated systems of polynomial equations, and often solve these polynomial systems with stunning speed and accuracy.

      The arrays here, working in combination with some switching elements, can solve such polynomial equation systems.   The arrays and patterns set out here are simple, and should be of widespread biological interest, either as direct models of nerve tissue or as analogs to biological function.

     The arrays are fast.   Most of the computation in these networks is massively parallel.   With the neurons in the arrays working at ordinary neuron speeds, these array systems should be able to execute complex calculations as quickly as animals actually do them.   These array systems also work with other systems, such as Parallel Distibuted Processing (P.D.P.) networks.

      The arrays shown here convert patterns to codes.   Matched and inverse arrays convert codes back to patterns.   These matched arrays, along with some supporting arrays, make possible a broad class of geometrically, logically, and linguistically oriented neural code systems.   The arrays are particularly adapted for rapid recognition and manipulation of faces or other image forms.

     These array systems⁽²⁾ also form a link between "symbolic" and "connectionist" theories of memory and neural processing - a link that is badly needed on functional grounds.   These codes and supporting array systems also suggest requirements for memory storing and logic manipulating neural structures (Lynch⁽³⁾, Shepherd⁽⁴⁾, Black⁽⁵⁾).   The encoding produced by these systems may permit classification and storage of "objects" and object categories with many fewer neurons or neuron components than might otherwise have been expected (Newsome, Britten, and Movshen⁽⁶⁾).   These code systems may also suggest alternative codes and array-code systems.   Whether or not these models map to specific parts of vertebrate brains, consideration of these models, and particularly consideration of the restrictions that are needed for these models to operate in computational detail, may guide further theory.

     The mathematical basis of these array systems is the very old mathematics of finite differences.   In Napoleonic France, this math was used by teams under the great M. Legendre to construct many mathematical tables of high accuracy⁽⁷⁾.   In 1821, Charles Babbage used this mathematics to build his "Difference Engine #2," a forerunner of the modern computer (Bromley, 1982).   Babbage based his machine on finite differences because "mathematicians have discovered that all the Tables most important for practical purposes, such as those related to Astronomy and Navigation can ... be calculated ... by that method."⁽⁸⁾

      An example of Babbage's finite difference table organization is shown below at the left. (Legendre's organization was the same as Babbage's.)   The finite difference table sets out values and differences for the series x⁴ for integer x from 0 to 13.   This organization is embodied in the mechanical linkages and dials of "Difference Engine #2."   Notice that each column is one number shorter than the one to its left⁽⁹⁾.

     At the right below is the similar but usefully different array structure used in this paper. These "diffterm" arrays retain the top (italicized) numbers in the successive difference columns that are thrown away in the Legendre-Babbage formulation.


Legendre-Babbage formulation
 x         x⁴      D1      D2        D3      D4
1           1       15        50       60        24
2         16       65     110        84        24
3         81     175     194      108        24
4       256     369     302      132        24
5       625     671     434      156        24
6     1296   1105     590      180        24
7     2401   1695     770      204        24
8     4096   2465     974      228        24

Diffterm Formulation
x          x⁴      D1      D2         D3       D4     D5
0           0         0         0            0          0       0
1           1         1         1            1          1       1
2         16       15       14          13        12     11
3         81       65       50          36        23     11
4       256     175     110          60        24       1
5       625     369     194          84        24       0
6     1296     671     302        108        24       0
7     2401   1105     434        132        24       0
8     4096   1695     590        156        24       0

Other array examples, generated by taking differences of the series 1,2,3,4,5,6,8 . . . to the 0th, 1st, 2d and 3rd power are shown below. The blue numbers at the top of the difference (DN) columns, that would have been rejected by Legendre or Babbage, are retained in these arrays, and prove to be useful for array encoding and manipulations.

x0    D1   D2    D3    D4    D5
 0      0      0      0       0      0
 1      1      1      1       1      1
 1      0     -1     -2      -3    -4
 1      0      0      1       3      6
 1      0      0      0      -1    -4
 1      0      0      0       0      1
 1      0      0      0       0      0
 1      0      0      0       0      0
 1      0      0      0       0      0

x1      D1      D2      D3      D4      D5
  0        0          0        0         0        0
  1        1          1        1         1        1
  2        1          0       -1        -2      -3
  3        1          0        0         1        3
  4        1          0        0         0       -1
  5        1          0        0         0        0
  6        1          0        0         0        0
  7        1          0        0         0        0
  8        1          0        0         0        0
  9        1          0        0         0        0
10        1          0        0         0        0

x2       D1       D2      D3       D4     D5
  0          0         0         0          0       0
  1          1         1         1          1       1
  4          3         2         1          0      -1
  9          5         2         0         -1      -1
16          7         2         0          0       1
25          9         2         0          0       0
36        11         2         0          0       0
49        13         2         0          0       0
64        15         2         0          0       0
81        17         2         0          0       0

    x³      D1      D2      D3      D4     D5
    0           0        0         0         0       0
    1           1        1         1         1       1
    8           7        6         5         4       3
  27         19      12         6         1      -3
  64         37      18         6         0      -1
125         61      24         6         0       0
216         91      30         6         0       0
343       127      36         6         0       0
512       169      42         6         0       0
729       217      48         6         0       0
1000     271      54         6         0       0

All monomials (functions of the form xⁿ with positive integer n) have characteristic diffterm patterns. These patterns can be recognized as signatures. These signatures are separable, so that the diffterm of an unknown polynomial signal can be decoded to yield the polynomial coefficients of that signal.

     Diffterms arrays are therefore well adapted for storing geometrical information in compact coded form, for converting the stored, coded forms back into geometrical information, and for computations involving polynomial functions.     Computations involving polynomial functions can have many, many applications.

Algorithms used in this paper are modifications of the finite difference mathematics of Legendre and Babbage⁽¹⁰⁾. Additions permit rapid identification of the polynomial definition of a curve from data points. Modifications have also been added for frame of reference change, scale change, other transforms, and checking. All the algorithms proposed are adaptable to massively parallel computation. All can be mapped to plausible neural assemblies.

2. USES OF POLYNOMIAL SYSTEMS

    Most of the relationships in physics, engineering, and other science-based fields involve polynomials.   Polynomials are also useful for the encoding and manipulation of lines and images.   The polynomial format makes it easy to approximate lines to any desired degree of accuracy by a (usually small) number of polynomial arc segments.   Polynomial manipulations also make it easy to zoom or rotate or distort an image.   I suggest that image processing and geometrical calculation in the brain are similar to the processing of polynomial encodings proposed here.

   Polynomial coding also works for logical applications.   Polynomial encodings form direct transitions between the smooth, continuous world of quantity and the lumpy world of the symbol.

3. POLYNOMIAL MANIPULATING ARRAYS

      The most important arrays proposed in this paper are illustrated in Figures 1 and 2. These arrays are almost exact neural analogs of Charles Babbage's Difference Engine No. 2, except that they conserve the top numbers previously referred to so that they generate signature patterns such as the blue numbers shown above.

      The author rederived and extended the mathematics set out here without knowledge of the prior work of Legendre and Babbage.    The math here is so natural that rederivations should not be surprising.    Indeed, given enough time and a way of remembering working patterns, the derivation might occur at random.    I suggest that this has happened, and that all or most of the array systems that embody the mathematics here evolved between 600 and 400 million years ago.    Neural structures that appear to be able to do this mathematics (at least at the level described by Laughton) occur in all vertebrates, in all arthropods, and in all of the seeing invertebrates.   The neural structures involved require an autocalibration mechanism that appears feasible and that will be discussed briefly later.

4. NOTES ON SERIAL NUMBERS

Arrays such as that of Fig. 2, organized in systems, can encode image forms or other entities into unique and compact "serial numbers" in various database-like formats. The same storage and retrieval operations that work on other computer-treatable index numbers, such as book call numbers, telephone numbers, or words, can also work on these polynomial-based serial numbers. However, these serial number codes go beyond the classificatory function of the usual serial number, and also carry in them the information needed to reconstruct the images or entities that they classify.

     The notion of the "serial number" used here is a crucial one.   A "serial number" is an unbranched one dimensional (step by step) sequence of numbers or signs representable as numbers.    All printable language sequences, all computer programs, all computer data sets, and all technically useful classification codes are representable as serial numbers.    The Fig. 2 type arrays set out here encode curves compactly into the class of the serial numbers.    The Fig. 1 type arrays convert serial numbers so encoded back to curves or functions.

        Some may object that the serial number format, so necessary for man and woman-made classification arrangements, is not needed in a massively parallel brain.    The classifications in P.D.P. networks offer many examples of classifications that are not easily reducible to serial number form.   Data in these P.D.P. networks are notably nonportable, however⁽¹¹⁾. Nonportability means that these structures cannot be used for many of the most direct and useful kinds of comparing and contrasting.    These structures are also notably bulky entities for any form of memory.   For symbol level manipulations, serial number symbol formats are probably indispensable and are surely convenient.   Symbol processing manipulations are often or mostly sequential, and would still be so in a massively parallel system, because interactions in the world (particularly those interactions that can be well described by human or computer language) are often sequential.

      It should be noted that a symbol expressible as a serial number need not be stored in explicitly serial number form.   Instead, it could be stored as a parallel system of linked physical symbols. In a computer, for instance, numbers are stored with a separate piece of memory for each bit, but with specific rules for how a stored number may be reconstructed.   In a neural system, a piece of information reducible to the serial numbers could be transmitted in a number of logically linked nerve fibers.   The information in these different fibers could be handled differently for different purposes, sometimes in parallel form, and sometimes in sequence.

      The serial number formulations set out here tend to support the "grandmother cell" hypothesis, wherein "perceptual stimuli are categorized by means of a hierarchy of neural mechanisms terminating in the activity of a set of neurons, each of which is associated with a particular object".   The patterns set out here do not require any single cell to represent an object, and I would use the word "object" as "category of objects," with progressively narrower possible categorizations.   Nonetheless, the compactly encoded patterns proposed here should permit detailed information to be stored in one or a few cells, and would be consistent with experimental observations. (Newsome, Britten, and Movshon, 1989).

11. SYSTEM ASSUMPTIONS

This paper proposes that finite difference based arrays and related code devices function as widespread specialized and general purpose brain components. This proposal entails the assumption of some additional conditions, as follows:

1. The brain includes resources that can take encoded information from finite difference arrays

2. The brain can manipulate this encoded information into memorable form.

3. The brain can access this encoded information from memory.

4. The brain can manipulate the encoded information in many ways involving Boolean and linear algebra. and

5. The brain can place this encoded information into finite step integration arrays for regeneration for various purposes including but not limited to image processing and motor control.

      The models and examples that follow also assume the presence of polynomial manipulation apparatus in thousands, tens of thousands, or millions of separate places in the vertebrate brain.    The many-processor assumption implies the presence of a compatible code system that can coordinate many processors.

5. CALIBRATION

     The arrays set out here are sensitive to maladjustment.    Tables A and B below illustrate this sensitivity.   Table A is diffterm array.   In the first column are 0's, except for one "unit perturbation," or error.   Note how this error increases as it propagates into the higher order diffterm columns.   Table B is a finite step integration array.   In the D5 column are 0's, except for one "unit perturbation."   Note how the finite step integration process propagates and expands the initial error.   Finite step integration arrays are even more calibration sensitive than diffterm arrays.   Additional array errors would involve superpositions of these patterns on the arrays.   Diffterm or finite step integration arrays with many randomly superimposed errors due to miscalibration would be insensitive or useless. The transforms set out in this paper require calibration of array elements.

Table A:   Propagation of finite difference array error

N        D1     D2      D3      D4     D5     
0         0        0         0        0       0
0         0        0         0        0       0
1         1        1         1        1       1
0        -1       -2       -3       -4     -5
0         0        1         3        6       1
0         0        0        -1      -4    -10
0         0        0         0        1       5
0         0        0         0        0      -1
0         0        0         0        0       0
0         0        0         0        0       0

Table B :  Propagation of finite integration error:

            D1    D2     D3   D4  D5  D6
    0       0       0       0     0     0   0
    0       0       0       0     0     0   0
    1       1       1       1     1     1   1
    6       5       4       3     2     1   0
  21     15      10       6     3    1   0
  56     35      20     10     4    1   0
126     70      35     15     5    1   0
252   126      56     21     6    1   0
462   210      84     28     7    1   0
792   330    120     36     8    1   0

    Calibration is the subject of a companion paper in preparation.     It deals with calibration of the finite integration, finite differentiation, and parsing arrays set out in this paper, and also deals with the calibration of other kinds of neural networks and arrays.    It argues that the precise calibration of such arrays should be biologically feasible, and that evolution of calibration arrangements seems likely.

    To calibrate a diffterm or finite step integration array, one must zero each element of the array, and then set two coefficients (that may be called alpha and beta coefficients) for each array element. Calibration steps are:

1. Zero the array, so that output at each element is 0 when inputs are 0. Because of the form of the element response, it may be possible to do this once per calibration event. Otherwise, zeroing may require the sort of cyclic focusing familiar to most users of scientific instruments.

2. Set all the element coefficients (denoted alpha coefficients) that may be calibrated in column without dependence on the beta coefficients.

3. Set all the element coefficients (denoted beta coefficients) that may be calibrated in row without dependence on the alpha coefficients.

     Table C offers the patterns needed for finite step integration calibration.    Given a means to zero the array elements, the repeating sequence of 1's in the vertical direction from (6,3) offers a pattern that works for calibrating the column 6 (or column n) column-dependent alpha coefficients, given a step-by-step comparator.    In like fashion, the repeating sequence of 1's in the horizontal direction decreasing from (7,3) offers a pattern that works for calibrating the row 3 (or row n) row-dependent beta coefficients of a finite integration array, given a step-by-step comparator.

     The repeating 1,1,1,1,..1 row sequence in Table C serves in an analogous fashion as the calibration pattern needed for the beta coefficients of a diffterm array.    The following additional array manipulation (in addition to a zeroing procedure) suffices for the alpha coefficients.

Table C
    C4C5
 0 0 0 0 0 0
 0 0 1 0 0 0
 0 0 1 0 0 0
 0 0 1 0 0 0
 0 0 1 0 0 0
 0 0 1 0 0 0

This array arrangement requires that diffterm values be set up in a column (C4) that would never occur in actual operation to calibrate the next column to the right (C4).

       I have done programs that show the rapid calibration of initially randomized finite step integration and finite differencing arrays using simple and fast algorithms that use the patterns above.   In a paper (that I hope to prepare at a later time) I argue that these calibration procedures (along with some others) are necessary parts of higher neural function, and are biologically feasible and likely.   An argument being developed in detail concerns sleep: it is argued that some necessary calibration procedures, including those needed for calibrating diffterm and finite integration arrays, require the shutting down of the neural arrangements being calibrated, and that calibration is the purpose and indeed the substance of the sleeping state.

6. THE ARRAYS AS MATHEMATICAL CODE DEVICES

Polynomials can be code elements. Polynomials can conveniently describe curves. Please recall what a polynomial is. Here is a 5th degree polynomial (polynomial with 5 as the highest exponent):

This polynomial can be stored in a "database entry format" as six numbers:

                                             (.73, -1.4, 3, 1.2, -.8, 3).

Any 5th degree polynomial can be stored in, and reconstructed from, a similar 6-entry "database entry format."   The order used here happens to be the conventional one.   But any other order of coefficients would work as well from a code and reconstruction point of view if it were standardized.     Any nth degree polynomial (with n a whole number) can be stored in, and reconstructed from, an analogous "database entry format" with n+1 entries.

       Specification of an nth degree polynomial takes at least n+1 numbers.    Any specification including more than n+1 numbers can be condensed to the shorter n+1 entry form.   The n+1 numbers constitute FAR less information than that needed to specify the infinite number of points on the polynomial curve.

        The n+1 entries necessary to specify a polynomial can be shuffled into various combinations.    Some combinations will be easier to read than others; some will have more than n+1 entries, some will not.    Hard to read combinations can be called encrypted.

For example, the calibrated asymmetric lateral inhibition array of Fig. 2 calculates finite differences according to the pattern shown in the table below. The input or signal column of the table, column s, shows a simple polynomial,

or, in general polynomial form,

with x increasing in unit steps from 0.

Column D1 shows the first differences of the input signal column. Column D2 shows the first differences of column D¹. Column D3 shows the first differences of column D2. Columns D4, D5, and so on could be constructed in the same fashion.    All columns could, of course, be indefinitely longer than those shown.

 x²  D1 D2 D3  D4
  0    0    0    0    0
  1    1    1    1    1
  4    3    2    1    0
  9    5    2    0   -1
16    7    2    0    0
25    9    2    0    0

The bolded numbers in columns D2, D3, and D4 are encrypted database formats. The first three digits in column D2, (0,1,2); the first four digits of column D3, (0,1,1,0); and the first five digits in column D4 (0,1,0,-1,0) all encode the polynomial input function, s. Note that the last digit of the databases of D3 and D4 are zeros. The last digit of a D5 or D6 database would also be 0. Translated into "easily readable" polynomial database form, these encrypted database forms all carry the same message, which is

"(1,0,0)

or, more specifically

" From the boundary, the input signal to this finite differencing array is the equation y = x² +0x + 0, where the measure of x is the step interval size of this array."

The three digit database form of column D2 suffices to encode any polynomial of 2nd or lower order. The four digit database form of column D3 suffices to encode any polynomial of 3rd or lower order. The same pattern continues. For any integer n, no matter how large, the n+1 digit database form of column dn suffices to encode any polynomial of nth order or less.

All these database forms are encrypted in the sense that they do not reveal the polynomial coefficients of the encoded curve in separated coefficient form. The arrays shown in Figure 3 decode these database forms (do this coefficient separation). As the difference order N in Dⁿ increases, there will be a largest database form with a nonzero last digit. This last digit determines the highest order coefficient of the polynomial. For the n+1 entry encoding that will occur in diffterm column Dn,

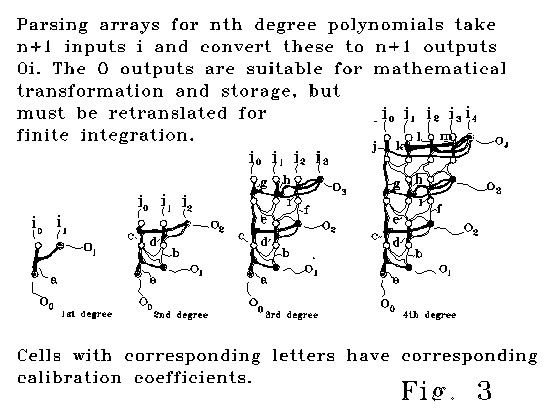
the last number will always be the coefficient of the nth order term of the polynomial input multiplied by n! (instances of the series 1, 1, 2, 6, 24, 120, 720, 5040, ...). The contribution of this highest order coefficient can then be stripped away from the remaining database numbers. This stripping can be done with little computation if knowledge of the database form of the nth order monomial is held in memory or embodied in decoder structure. An n entry database form now remains. The lowest entry in this database (that could, of course, be 0) will be the coefficient of the (n-1)th term multiplied by (n-1)!. Other database numbers corresponding to this (n-1)th term can now be stripped away. The next highest coefficient can be identified as the lowest database digit in the next database divided by (n-2)!) and then stripped away in the same fashion. This process can be continued until all the polynomial coefficients (including the constant or x⁰ coefficient) have been identified. The decoding is fast, and is as exact as the computation device used. The devices shown in Fig 3 do this decoding in a parallel-analog fashion. I have programs that do this same job digitally.

7. ARRAY SPEED AND ARRAY DECODING

The diffterm arrays (including array systems embodying millions of "cells") can be astonishingly fast compared to the speed of current computer-based techniques for calculating a readable polynomial database form from data points.

Diffterm neural arrays operate in parallel. Time for a system of cells in one of these arrays to reach equilibrium (and finish its computation) is roughly tau( m + d-1), where tau is the 1/e equilibration time of a "cell," m is the number of taus specified for "equilibration" of a characteristic element and d is the cell depth of the array. The table below shows a computer simulation of equilibration for diffterm arrays capable of handling polynomials of 5th degree or lower, assuming exponential equilibration of elements. The input to the array is perturbed at 0 time.

EQUILIBRATION FRACTIONS FOR 2 TAU STEPS AFTER PERTURBATION AT 0 TAU

                D1         D2            D3           D4            D5

0 Tau   0.00000   0.00000   0.00000   0.00000   0.00000
2 Tau   0.86466   0.60031   0.33603   0.15580   0.06152
4 Tau   0.98168   0.91018   0.76889   0.58056   0.39002
6 Tau   0.99752   0.98301   0.94017   0.85521   0.72779
8 Tau   0.99966   0.99705   0.98676   0.95968   0.90584
10 Tau 0.99995   0.99951   0.99734   0.99021   0.97255
12 Tau 0.99999   0.99992   0.99950   0.99784   0.99291


     Within 10 tau, a calibrated diffterm array would generate database forms for all coefficients of a 3rd degree polynomial good within .3%.   Within 14 tau, a calibrated diffterm array would generate database forms for all coefficients of a 5th degree polynomial accurate to within .2%.

     Nerve "cells" in asymmetric lateral inhibition arrays might not obey a simple 1/e equilibration law.    However, for any plausible law, equilibration times would increase with Diffterm column depth in a similar way for basic dimensional reasons⁽¹²⁾.   For nerve cells the value of tau should be of the order of 1 millisecond or less.   For an analogous system constructed of VLSI circuit elements, tau might be about a nanosecond.

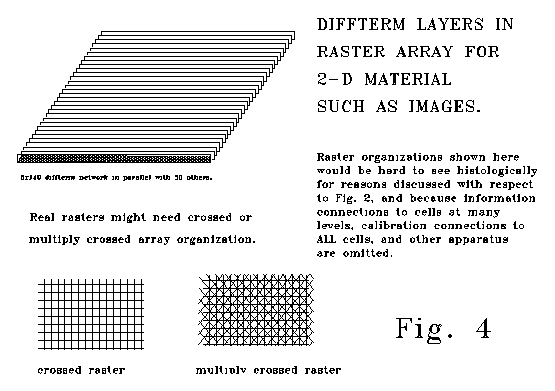
      The results of the table do not depend on the length (as opposed to depth) of a diffterm array, nor do they depend on the number of diffterm arrays operating in coordinated parallel fashion.    A raster assembly of diffterm arrays such as that illustrated in Fig 4. might embody fifty million (or half a billion) individual cells at a cell depth of m.   Because of parallel circuit equilibration, such an array would come to equilibrium in the same time as another array, also of depth m, embodying only a few tens of cells.

      Large parallel neural network diffterm arrays can compute much more rapidly than a fast digital (step by step) computer calculating according to the same finite difference pattern can. Assuming single precision computation, the computer will have to do at least 20 digital operations (involving computation and memory) for each "cell."      Therefore, array calculation time is about

time = 20 N_c time/cycle

where N_c is the number of "cells."     For an array capable of high resolution image processing, (a 10,000 x 10,000 pixel array with a depth of 4) and twenty nanoseconds per digital operation, the total time to compute the array would be eight seconds.    The analog array would equilibrate to the five tau (.7% error) level in eight milliseconds (tau=1 msec).    Here array equilibration with a neural network is one thousand times faster than the analogous digital computation, even though the individual neurons are roughly 50,000 times slower than the digital computer's cycle rate.

      The neural network computation is done without switching operations, and does not require the huge memory capacity and memory transfer that the digital computer needs to do this job.

       The decoding arrays shown in Fig. 5 are similarly fast.   For a decoder adapted to decode databases for polynomials of nth order or less, the number of taus for an m tau level equilibrium of the least accurate coefficient is roughly m+2n-1 where n is diffterm array depth, the maximum order polynomial decoded.   In the table above, error fractions in column D3 would correspond to error fractions for a 2nd degree decoder, error fractions in column D5 would also correspond to error fractions in a 3rd degree polynomial decoder, and error fractions in column D7 would correspond to error fractions per unit time in a 4th degree polynomial decoder.   Any number of these decoding arrays could be acting in parallel without interfering with each other. Again, nerve "cells" might not obey a simple 1/e equilibration law.   However, for any plausible law, equilibration times would increase with polynomial order roughly as shown for basic dimensional reasons (Kline, 1965).

8. USES OF THE "ENCRYPTED" AND "DECODED" DATABASE FORMS

The separated coefficient form of the polynomial specification generated by the decoding grid is needed for rescaling, interpolating, extrapolating, rotating, or distorting the specified function, or for almost any other manipulation we would normally use algebra to do.

The "encrypted" form of the polynomial specification that comes directly from diffterm array is also useful. This "encrypted" form is used to regenerate an nth degree polynomial from its n+1 specification numbers using an array such as Fig. 1.

9. FINITE STEP INTEGRATION ARRAY SPEED AND SCALING

The finite step integration arrays are parallel devices, and are also fast by step-by-step computational standards. Still, they are slower than diffterm array systems because they are length sensitive. The formula for equilibration time to the m tau level in the least accurate cell of such an array is roughly

time = m + (d-1) + L

where d is array depth and L is the step length of the finite step integration. For long step integration lengths, L dominates equilibration time.

     These arrays are also subject to the rapid buildup of errors, so that a finite step array must be precise if it is to accurately regenerate a polynomial over a large number of steps.   Accuracy and time pressures would be expected to shape biological embodiments of these arrays.   A high performance system of these arrays would be expected to exist at several linked scales, so that relatively long integrations could occur (quickly) in a relatively few large steps, with fine scale interpolating integrations also occurring quickly between the larger steps.   Such linked scales would also be useful for system calibration.

10. ONE TRIAL LEARNING

The coded networks shown here do not inherently require repeated training.  At the first trial, inputs to these systems generate an immediately clear encoding.

14. SUBSIDIARY PROCESSES

Several subsidiary processes are needed for various system applications:

1. System scaling

1. to zoom a polynomial to fit step intervals different by a factor of M C_iz =M^-i C_i

2. to shrink-expand by a factor of M on the abscissa axis without changing ordinal length, C_is= M C_i

a. This transform is the same as rotation about the ordinal axis by an angle theta when M=cos(theta) .

3. Rotation about the abscissa axis is equivalent to a combined zoom and shrink-expand step.

2. Z axis rotation. Let x₁ be the original ordinate axis and y₁ = f(x₁) be the original abscissa value. Rotation about the z axis by an angle theta works with the transforms:

x₂ = cos(theta)x₁ + sin(theta)(f(x₁)) and

y₂ = sin(theta)x₁ + cos(theta)(f(x₁)).

3. Simple combined formulas permit an arc or polynomial to be zoomed or distorted, and also rotated about all three axes. The zoom formula is often useful for extrapolation or interpolation of functions.

5. The system is adapted to frame of reference change.   For an nth order polynomial, any n+1 points generated by (any scale of) finite step integration suffice as input for a recalculation of the function at the new frame of reference of the first of these n+1 points (if readout direction the new function is to be maintained) or the last of these n+1 points (if the readout direction is to be reversed).

6. Lines and systems of lines (images) are adaptable to a multiplicity of compact and searchable database forms.    To conserve space and make efficient searching possible, several kinds of database "normalization" are necessary and others may be highly useful.    The most basic normalization is scale normalization.

   Image recognition and comparison is far easier if images are stored at a standardized scale. With this scale standardization, the amount of data that must be stored and searched is decreased by a large factor, compared to the case where each separate scale must be searched separately.   Computational loads are also reduced.   Other sorts of normalization can also usefully compress data.   For planar geometry, a curve can be normalized for both scale and x and y axis rotation.   For example, consider a particular curve (or family of curves) displayed on a plane.   By variously changing the scale of this plane, an infinite set of polynomial descriptions could be generated.   Similarly large and diverse sets of descriptions might be generated by rotation of the line-displaying plane about the x and y axis.   However, the line descriptions generated by all such rotations and scaling changes could be collapsed into a single searchable family as follows.

1. Rescale curves to normalize curve ordinal length to some set value.

2. Multiply the curve (or curve system) coefficients so that the sum of these coefficients equals a set value (this transform, which is equivalent to rotation, could be replaced by other standardized transforms).

The normalization and rotation factors of steps 1 and 2 could be stored so that these transforms were reversible.   After these two normalizations, the previously "infinite" set of curves would collapse into one curve family, with N+1 identical serial numbers, that could be compared to other similarly normalized and encoded curve families.   There may be many different data compressions and abstractions of this sort.   The point is not to claim uniqueness or superordinate efficiency for any particular abstraction.   Rather, the point is that these condensation schemes exist, and can radically reduce the storage and retrieval tasks a neural system faces.

Calculus and differential equations

      As the step size of a diffterm array becomes smaller, "approximate integration or differentiation" approaches the exact performance of the infinitesimal calculus in the limit. "Approximate integration" or "approximate differential equation solution" with the finite step arrays works for multiple integrations or for higher order derivatives, and is adaptable to all the standard kinds of boundary condition manipulation.   Exact results of the diffterm and finite step integration formulations also generate formulas close to those most useful in calculus.

       In practical and scientific applications, by far the most important and most often used tools from calculus are the monomial integral and derivative formulas.    

The polynomial series formulations for sines and cosines and the immediately derivable integration and differentiation formulas for these trig functions are also important and might be fairly easily evolved.   Every addition term of these trig relations adds to the accuracy of spacial computations.

A moderately intelligent diffterm array equipped neural system with memory could derive these formulas. For example, see Fig ( ). In this case, the "encrypted" database definition for y=x², (0,1,1), is placed in the D4 rather than the D3 column of a finite step array. The function y=x² is formed in the D1 column, rather than the signal column. In the signal column is a finite step integration of the x² function.

If this integrated function is converted to a polynomial, it will be the familiar sum of the power series. The general sum of a power series relation is shown below.

The first term of the sum of a power series function for any monomial is always the correct monomial integration formula. The lower order terms are errors from an infinitesimal point of view, and should be thrown away. The situation with the infinitesimal derivative formula is similar, with lower order terms in error.

       The pattern set out above, wherein the database form (0,1,1) was put in "too high" a D column shows an example of a "Difference equation."   The analogy between difference equations and differential equations is close.   The differences between these formulations are systematic and predictable.

     I have a computer program that demonstrates that the diffterm and parsing apparatus correctly identifies sums of power series for exponents up to 13 within computer (10^{-13 decimal place}) precision. The array system would identify the coefficients of any other polynomial of like order equally quickly and well. Use of the same logic should make it possible to calculate and learn the power series formulations of the sine and cosine formulas.   These may be differentiated or integrated using the monomial formulas above.

     The mathematical facility that might be compactly encoded into a diffterm array system with memory and mastery of the most simple relations of calculus is large.    It is suggested that this sort of facility has had time to evolve.    I suspect that diffterms have been built into animal neurology for at least half a billion years.

12. DIFFTERM SYSTEMS IN A CONNECTIONIST CONTEXT

         A conflict has grown up between many "connectionist" modelers and people who have thought about brain function from a symbolic perspective. The older symbolic perspective traces from George Boole⁽¹³⁾ and earlier philosophers, and is congruent with both natural language reasoning and computer programming.    However, the symbolic perspective has been denounced as a "Boolean dream"⁽¹⁴⁾.   Primary objections to the symbol-level perspective have been set out as follows by Paul Smolensky⁽¹⁵⁾:

"      From the perspective of neuroscience, the problem with the symbolic paradigm is quite simply ... that it has provided precious little insight into the computational organization of the brain.     From the perspective of modelling human performance, symbolic models, such as Newell and Simon's General Problem Solver (1972), do a good job on a coarse level, but the finer structure of cognition seems to be more naturally described by nonsymbolic models.   In word recognition, for example, it is natural to think about activation levels of perceptual units.     In AI, the trouble with the Boolean dream is that symbolic rules and the logic used to manipulate them tend to produce rigid and brittle systems."


        The models here reinforce the "Boolean dream", using widespread neural arrays that will, if calibrated, generate and use polynomial-based code-symbols.    These arrays seem to provide direct insight into how the neural organization of the brain could do Boolean and linguistic symbol operations.    These arrays fit a broad class of database forms that would be useful for many kinds of pattern recognition.    These arrays and systems work for the recognition of visual forms (such as faces).    These same array-systems could perform most of the recognition tasks an animal does. The database forms involved are not inherently rigid or brittle, partly because they may involve connectionist-style neural subnetworks in many parts of their processing and learning apparatus. These code systems can operate in parallel rather than sequential mode, and can exhibit systems of "soft" as well as "hard" constraints.    

     The array systems set out here work for polynomial processing, including processing at the level of calculus and differential equations. These arrays can interface with previous array systems (notably Hebbian and backpropagating systems)(Hebb date) (Rummelhart, Hinton, and McClelland,date) that do statistical learning, boolean algebra, and linear algebraic manipulations (particularly those involved in classification).     A combined system capable of logic, classification, algebra, linear algebra, calculus, and statistical learning seems more desirable (and biologically more sensible) than any one system alone.

        The model system set out here should be complementary to previous connectionist work at the "hardware" or "computer paradigm" level.    Even so, the system should reinforce the "Boolean dream" that neural logic is largely a mathematically and logically comprehensible business of symbol manipulation.

Example cases of the "polynomial behavior" made possible with the finite difference arrays are set out below.



VISUAL AND LOGICAL CODE IN AN ANIMAL CONTEXT

       It is instructive to focus on the complexity and power of human and other animal pattern-recognition and manipulation.   The limitations of current machine image processing may make us focus on the difficulties of relatively simple image handling.   It is proper that we do so, but we should not forget how sophisticated and logically coupled animal and human image processing really is.    We thereby underestimate the tasks neural processing must do. Patent searching offers an impressive and clearly observable example of animal image processing capacities in combined form.

       Patent examiners and other searchers look through large, organized piles of drawings. While searching, a trained patent examiner (such as Albert Einstein was) interprets about one patent drawing per second.    A trained patent searcher will search a patent drawing, and correctly rule on its relevance in the context of a case, in about the time that searcher would have taken to read five words.   Trained searchers routinely cover 20,000 separate (and usually multi-figured) patent drawings per day.   For each drawing, the operational question "Does this drawing relate to the invention being searched in any important way?" is asked and answered. The number of database-like decisions that go into this process of drawing interpretation must be prodigious.   The manipulations of patent searching involve both images and logic, and is mostly nonlinguistic.

     The patent drawings a searcher processes are interesting in themselves.   Patent drawings have evolved under heavy pressure for readability.   It seems probable that the drawing conventions used at the U. S. Patent Office and other major patent offices are a close match to human image processing biology.   Patent drawings are stark black and white line drawings drawn on very white paper.   These drawings fit the visual model set out here.

      One patent drawing convention connects directly to the "object identification" logic proposed here.    Patent conventions encourage an absence of shading in contexts where the distinction between material and the "empty space" of background is "patently clear."    This occurs when a closed curve has some other closed curves or lines within it. I propose that this drawing convention connects to a primary image processing mechanism in vertebrates.

      The capacities shown by patent searchers, and some other familiar animal capacities, may relate to the examples set out here.

CASE 1: FUNCTION ENCODING AND EXTRAPOLATION FOR PREDICTIVE CONTROL

Given a receiver system, (that may map to a spatial plane or may record as a function of time) an Nth order polynomial can be identified after input of N+1 data points. The N+1 number database can be transferred into a finite step integration array of the same step scale (or, after decoding, rescaling, and recoding, into a differently scaled array). Integration in this array is likely to occur much faster than the event itself. This simple array system can predict the future within the limits of input function validity. This "prediction of the future" is broadly useful. It is useful whenever phenomenon that can be well or perfectly predicted by polynomials occur, for instance when a tennis player predicts the future positions of a ball. Polynomial phenomena permeate the natural world.

CASE 2: APPLICATIONS FOR POLYNOMIALS IN MOTOR CONTROL

         The time-integrated mean portion of a muscle fiber control curve can be mapped to a polynomial or short system of polynomial arcs.   The mapping is as compact as it mathematically can be.   Systems of such encoded muscle control arcs set out in database form can be coupled into larger database forms.   Rescalings, retimings, and various controllable distortions of these encodings are possible with convenient transforms that could be handled over a range of logical control levels.   Some useful details of such mapping and control are discussed with respect to the analogous transforms of image processing.

CASE 3: GENERATION OF A LINE DRAWING FROM A FULL IMAGE:

      Suppose a raster arrangement of finite differencing arrays such as that shown in Fig 6 is connected to an array of calibrated photosensors at the input level, after the manner of a retina. The finite differencing arrays in the raster will have different representations of the image at different column depths. At the level contacting the photosensors an "unprocessed" pixel image will occur. At each successive level, one polynomial order of the image will be encoded in a fashion that can be said to "remove" the order (except for the first N digits from the discontinuity for the Nth layer). But nonpolynomial information, especially discontinuities, will be propagated to the next layer. After n column layers, where n is array column depth, the image will be reduced to a "line drawing." Given accurate system calibration, the "line drawing" will store enough information to regenerate the image. Given less accurate calibration, the system will still generate a "line drawing" of the original image. This paper assumes that it is these line drawings, rather than full images, that are encoded in the brain.

CASE 4: CONTRAST SENSING

Diffterm arrays act to "strip away" one monomial term from a function at each diffterm layer, while propagating discontinuity information from layer to layer (for example, in an array such as that of Fig. 6). This means that a tightly calibrated diffterm array is a sensitive contrast sensor. In Fig () below, a single input of .1 is superimposed on the function x⁴ at 7⁴ = 2401. See how this discontinuity of one part in 24,010 stands out in the D5 and D6 columns.

        x⁴             D1           D2        D3         D4        D5       D6
        0.00          0.00        0.00      0.00       0.00     0.00     0.00
        1.00          1.00        1.00      1.00       1.00     1.00     1.00
      16.00        15.00      14.00    13.00     12.00   11.00    10.00
      81.00        65.00      50.00    36.00     23.00   11.00      0.00
    256.00      175.00    110.00    60.00     24.00     1.00   -10.00
    625.00      369.00    194.00     84.00    24.00     0.00     -1.00
  1296.00      671.00    302.00   108.00    24.00     0.00      0.00
  2401.10    1105.10    434.10   132.10    24.10     0.10      0.10
  4096.00    1694.90    589.80   155.70    23.60    -0.50     -0.60
  6561.00    2465.00    770.10   180.30    24.60     1.00      1.50
10000.00    3439.00    974.00    203.90   23.60    -1.00     -2.00

The contrast sensing property of diffterm arrays would be useful for the many animals whose survival depends on sensitive visual discriminations. The contrast sensing shown here requires accurate calibration and also offers a biological incentive for calibration.

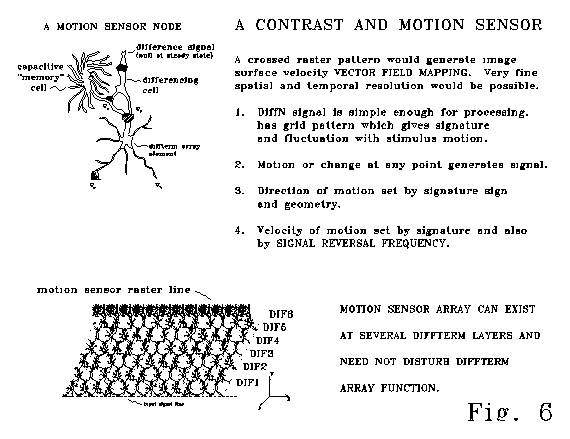
CASE 5. CHANGE AND MOTION SENSING

     The diffterm arrays shown so far are fast dynamic response devices, but do not emphasize or specially encode motion or temporal change.    Special motion and change encoding arrangements must be expected to exist for computational reasons.   Without specific adaptations for emphasizing temporal change or motion, the data processing loads involved in much vertebrate function would be thousands or millions of times greater than the data processing loads that would be needed with efficient motion or change sensing.

     Fig 6 shows an adaptation of the basic diffterm structure for sensing contrast and motion.   Fig 6a shows a motion sensor node.   The node consists of two differencing "cells" and one passive "cell" adapted with an extended surface and functioning as a capacitive memory element.   Such a capacitance element might be a glial cell, or might be an electronically isolated, high capacitance arborized section of a single cell.   At steady state the difference signal between the diffterm element "cell" and the capacitive memory "cell" will be zero.   During any period of signal change, this "motion sensor" node will generate a signal.

    An apparatus involving a capacitive memory cell and a differencing cell could work without being part of a diffterm array.     However, the diffterm array has large advantages for motion and change sensing.   One advantage is the stark relief offered by the polynomial extraction aspect of diffterm function.   Motion sensing arrays on a higher order diffterm column will be sensing a geometry that has already been sorted to emphasize discontinuities.   This "line drawing" array pattern is geometrically much simpler than the initial image, and will involve well separated signals much easier to process than the crowded signals generated from a full image.

    The "grid" generating nature of the diffterm mathematical structure illustrated in Fig 6b offers another advantage.   A single difference a in an input signal propagates through successive diffterm columns in the following manner:

0    0      0      0      0
a    a      a      a       a
0   -a   -2a   -3a   -4a
0    0      a     3a    6a
0    0      0     -a    -4a
0    0      0      0       a
0    0      0      0       0

      An initial disturbance of one sample width in the signal generates a magnified and alternating sign signal of N+1 steps in width in the Nth order diffterm column. This means that a moving discontinuity will generate a moving grid of N+1 step widths in the "instantaneous" Nth Diffterm grid. This moving grid will be superimposed on a relatively "stationary" (decaying) grid signal in the high capacitance memory array.   Motion of one grid across the other will generate a frequency signal, after the manner of a Moire pattern.   The output from such a system will involve signal reversals every time the input signal crosses a photosensor (in the human, about 120 reversals per degree across the fovea). Consider for simplicity a rectangular grid.   A moving point would be characterized by an x-direction and a y-direction planar visual velocity, each expressed as a frequency.   The proportionality between frequency and visual plane velocity for such a system depends on the regularity of sensor spacing, which is typically regular for visually competent vertebrates.   For a moving object with finite area and hence curvature, phase shift between rasters would generate additional information.

     This frequency-generating system has powerful advantages for an animal dealing with motion in space.    The frequency signal, the contrast signal, and the main image signal from a visual system can be superimposed to form a vector field mapping on the visual plane, wherein a surface velocity vector corresponds to every pixel point on each image line.

     Consider the information such a vector field mapping would hold for a moving animal.   With respect to a flat plane such as a ground or water surface, velocity vectors perpendicular to the main direction of motion would be zero at a line defined by the intersection of the ground or water plane by another plane defined by the line of motion and the line perpendicular to the earth.     Perpendicular velocity vectors would increase linearly with distance from that zero perpendicular velocity line.   Here, frequency information provides essential orientation information in compact form.   An animal moving directly into a plane surface would see zero spatial velocity directly in the direction of motion, and a circularly symmetric velocity vector field elsewhere on the plane.   With respect to a more complex environment, such as a jungle canopy, surface velocity vectors for objects the same distance from the animal would increase in circular fashion away from a no-surface-velocity point corresponding to the exact direction of animal motion.   In such an environment, angular motion per unit approach would provide sensitive information about the distance of various objects in the complex three dimensional space surveyed by the eyes.   This information would be of great use to an orienting animal, for example a landing bird, a brachiating monkey, or a soccer playing human. This information would also provide depth information for the many animals (including fish, birds, and the nimble horse) that have eyes so widely placed in their skulls that binocular overlap is limited or absent.

     The vector field processing proposed here is massively parallel and inherently fast.    The vector field information proposed could be used with direct and computationally derived information from other channels, for instance the parallax, proprioceptive, and visual channels, and would also serve to inform more complicated forms of geometrical reasoning and computation.    The contrast sensing arrangement here could work as part of a large system capable of rapidly sensing changes in a relatively few pixels out of a field of tens of millions of pixels, as people and animals can do.

CASE 6: CONVERSION OF A LINE DRAWING INTO A POLYNOMIAL ENCODING

STEP 1: SEARCHING  We don't know how it happens, but we do know that animal evolution has involved strong pressures for both visual speed and visual resolution. Together, these pressures have imposed the development of parallel and enormously effective visual searching arrangements.  Somehow, these arrangements can search pixel arrays comprising millions of pixels, and can do so in a few tens of milliseconds.   It should be emphasized that the job of searching an image is different from the job of encoding that image.

     I propose that the system of "simple," "complex," and "hypercomplex" cells shown by Hubel, Weisel, and those who have followed them function is a searching apparatus rather than an encoding apparatus.    These cell systems combine to form "line detectors," and "slope detectors" - exactly the inputs that the encoding system set out here needs.   Alternative encoding systems are likely to need the same slope and positional information.   Some may feel that searching is somehow a less important or less extensive task than encoding.   The issue of "importance" is based on a misunderstanding - searching is essential before encoding is possible.   Moreover, the task of searching is much more extensive than the task of encoding information once it has been found and reduced to encodable form.  In my opinion, searching a large field such as the visual field, the computational investment (in bits per second) devoted to searching is likely to exceed the computational investment devoted to encoding by at least two orders of magnitude, and is likely to require more complicated arrangements than the encoding requires.    Here, we talk about the inherently simplier job of encoding.

ENCODING OF A LINE DRAWING INTO POLYNOMIAL FORM FROM PRE- SORTED INFORMATION:

    A line drawing image can be encoded as a system of polynomial arcs, with the connections between arcs in the system specified.    Because polynomial specifications of a line are unsatisfactory when the line approaches perpendicularity with the ordinal line, more than one coordinate system is necessary to specify all lines.   In a rectangular array, functions of perpendicular directions x and y are most convenient. Axes 60 degrees apart would work well also, and would be well adapted to the hexagonal packing array often found in cells.

      In a rectangular array of pixels, slopes that may occur between adjacent pixels are  0, 1, infinity, -1, 0, 1, infinity, and -1. As a function of x, it is useful to first encode arc systems that go from a slope of -1 to 1 and also to encode arc systems that go from slope 1 to -1. (These arc positions should be fed to the processing system by the search apparatus.) As a function of y, a roughly perpendicular class of arcs would be encoded between the same numerical slopes.

Although 3rd, 5th, or other degree equations would also work, it seems reasonable to encode these arcs as 4th degree equations.    4th degree encoding means that each arc requires 5 data points (the beginning, the end, and three evenly spaced intermediate points, so that the curve is divided into sections, each of 25% of ordinal length).   The intermediate points may fall between pixel data points, in which case values are found by interpolation.   In addition, it is useful to gather 4 "curve check" points intermediate to the five data points.   From the five data points, a diffterm array finds an encoded form of the polynomial that exactly intersects with the five given points, with the polynomial set out on a step interval 1/4th of the ordinate length of the arc.   This encoded database form is then converted to the separate coefficient database form.   Coefficients are then rescaled (after the manner of Case 3 above) to match the step interval scale of the pixel spacing.

      The arc produced at this stage will usually be a good approximation of the true arc system between the image arc's beginning and end points (within pixel resolution).   However, the curve may smear out details.   Calculation of the function values that correspond to the "curve check" points, and comparison of these calculated values with the "curve check" points, will often identify curves that need to be encoded to a finer scale.

For a curve in need of finer encoding, a point for point subtraction between the input curve and the polynomial approximation curve will yield a difference curve.   Local maxima of absolute differences along this curve, plus curve beginning and end points, will specify the arc end points for the end-for-end system of finer scale arcs.   Polynomial approximations of these arcs, taken together, will encode to a "perfect" arc system approximation within the limits of pixel resolution.

On reversal of ordinate and abscissa, the system for encoding functions of y is the same as that for encoding functions of x.

The encoding processes set out here could occur in parallel, and biologically would have to do so.   According to this pattern,  at least hundreds and probably many thousands of separate encoding systems must be operating simultaneously while a higher vertebrate is seeing.   Even with highly parallel encoding systems,  encoding effort will still be a biologically scarce resource that will require allocation via some "selective attention" mechanism.   This may be one of the reasons that a seeing animal cannot pay attention to everything in its visual field at any one time.

Storage of the lines at this stage of encoding requires, for each line, construction and storage of a database format containing the arc beginning point, arc end point, five coefficient numbers, and line darkness. Storage of such a database for each line in the line drawing suffices to encode the image. However, there are additional pieces of information that would assist in further encoding. These may include (in x and y coordinates) xmax, xmin, ymax, ymin, end point coordinates, and "identification numbers" that match the "identification numbers" of lines that the encoded line is touching. These additional pieces of information will be useful in object recognition and classification, discussed in cases to follow.

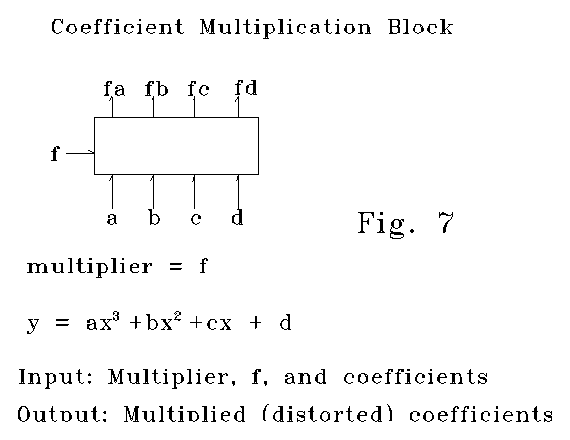
     Neural network systems to do the line encoding set out here can be identified. Five data point voltages or frequencies (beginning, end, and three interpolated voltages or frequencies) can be put into a 5 layer diffterm array consisting of 25 cells, that will convert the input equation form into an "encoded polynomial form."   This encoded polynomial form can be converted to a separate coefficient form by a parsing array such as that shown in Fig  3.   The separate coefficient array can be rescaled to pixel scale using an array such as that shown in Fig 7.   This rescaled coefficient array can be re-encoded by an array such as that shown in Fig 5.  The re-encoded array inputs can be placed in a finite step integration network to generate the polynomial approximation curve related to the curve being coded, for acceptance or later interval refinement. This paragraph, taken alone, is plainly not specification of a system.   The "raw" encoding here has limitations.   This first stage of encoding is not adapted to recognition tasks, but it is a beginning to encodings that are adapted for recognition tasks.

CASE 7: CONVERSION OF A "RAW" IMAGE ENCODING BACK TO A LINE DRAWING

       Given the "raw" encoding set out in Case 4, reconstruction of an image is straightforward. The database representing each arc would be taken from storage, and converted to an arc on the image plane using a finite step integration array and means to position the beginning of the arc.   Once all the database encoded arcs were decoded in this way, the image would be reconstructed.   Using the transforms set out in "Subsidiary Processes" (14) above, the transforms needed to rescale the image, or rotate the image about the x, y, or z axes are also clear.   The storage capacity required for the polynomial encoding of an image is much smaller than the computer storage capacity needed to store the original image in conventional pixel-by-pixel form.

CASE 8: FIRST STAGES OF OBJECT IDENTIFICATION: ENCODING FOR RECOGNIZABILITY AND MANIPULATION

An "object" may be defined here as a pattern of data that organizes more than one data structure into a form that can be handled (searched, manipulated) as a unit. Examples of objects might be faces, letters, houses, hands, etc. An "object" is itself a data structure. A data structure is an entity with a beginning, an end, some organized pattern or sequence for the holding of data (or smaller data structures), and some practically workable tag or tag system that can be used for storage and retrieval. For example, the data structure needed to encode a 4th degree curve in a fashion adapted for further processing might be the sequence

"curvetagstart/0thcoef/1stcoef/2ndcoef/3rdcoef/4thcoef/xmax/xmin/ymax/ymin/curvestartx/curvestarty/curvendx/curvendy/curvetagend"

where the separator / is a sequence of numbers or other tag means that divides and labels the data. The serial number 67151452353125411559. . .620 might designate the equation y=4+3x+ 12x² +11x³ +9x⁴, with 671=curvestart, 620=curveend and labelled separators 51, 52, 53, 54, 55, 56 and so on.    For other purposes, this particular curve may be given a "name," such as "C8."   Although the pattern abstracted above may seem artificial, a symbol-manipulating animal manipulating any memory system that can be thought of as a database would be manipulating codes mappable to serial numbers in a fashion similar to this.   The use of names is an example of data abstraction (the hiding of total system complexity so that the system may be manipulated more efficiently).   For some general purposes, all curves might be dealt with at the abstracted level of "curves," that might be labeled "c." (The abstraction "c" has most or all of the basic properties of a noun in language.)   It should also be noted that not all of this serial number form needs to be searched for all purposes.   For instance, searches that do not search exact visual field position information deal with a "new" data structure abstracted from its visual field position.   Many other useful kinds of abstraction are also inherent in the nature of data structure manipulation.

     Efficient image storage and recognition requires that images be organized as specialized "objects."   The most primitive object form seems to be made up of a closed curve and the other curves (whether closed of open) that this closed curve contains.   This object pattern corresponds to the patent drawing convention set out before.   This most primitive object form may be processed (and classified) further, and the information in the primitive object may be reorganized in more specialized object forms (for example frontal face database forms, profile face database forms, animal body profile database forms, frontal automobile database forms, tree database forms etc., etc.).   An object may include sub-objects (for instance, faces have eyes, trees have branches, cars have doors that have handles, etc). Sub-objects may have sub-objects in turn. The classification "search keys" (database search characters) useful for different speed and precision searches will differ. Objects that are similar or identical for some purposes will be different for others.

      These more complicated objects may be processed from the primitive objects.   Before these primitive objects can be formed, closed curves must be identified.   It must be established which closed curves are inside which others.   It must be established which unclosed curves are within which closed curves.   The arc labelling needed for this searching is straightforward if, during the initial arc encoding, the following data are stored for each arc: maximum x value, maximum y value, minimum x value, minimum y value, and an "identification number" that will be the same for any two curves in contact with each other. "Identification number" matching then permits formation of sets of connected arcs.   If tracing from "beginning points" to "end points" of curves in a set results in a repeating sequence, then a closed curve has been identified.   Once a closed curve is found, it is a straightforward search to identify arcs (closed or open) that probably fall entirely within that closed curve, using xmax, xmin, ymax, and ymin values for each arc.

Normalizations: The transforms set out in SUBSIDIARY PROCESSES (14) are useful for object normalization. Normalization of objects to a standard scale renders visual images seen at different scales comparable. Normalizations for various kinds of plane rotation are also useful ways to radically reduce the amount of data that must be stored and searched. Many normalizations and data transforms can compress data structures. Different compression patterns fit (or can be used for) different contexts.

      Efficiency dictates that primitive object identification and some standardized object normalization be done prior to further processing and subclassification of image information in any complex system.    I have a simple image processing program, that scales faces to a standard scale to facilitate recognition and processing.

If one accepts the plausibility of the diffterm scheme set out here, it seems likely that highly visual animals such as man have hundreds or thousands of parallel systems capable of forming scale-normalized primitive objects in their visual apparatus.   For efficiency, these systems should be organized geometrically and at different scales, with some subsystems processing courser and larger scale information than others.

     Once images have been processed into scale-normalized primitive objects, many additional processing patterns that could generate useful specialized object forms become possible.  Most of this processing could be done in parallel.   Many patterns capable of the organization required for new object processing could be made of simple connectionist nets, including backpropagating nets.

   For example, I believe that a "human face recognizing" program could be constructed in this way, and that the program could learn what a face looked like, and develop a more an more sophisticated set of discriminating tests for face recognition, in a way showing many of the characteristics of human learning.   I hope to find support that permits me to do such work. I believe that similar logic would permit recognizers of other classes of objects top be fahioned as well.   Because polynomial processing can normalize the objects observed, faces (or other objects) that are identical except for scale and placement would have "serial number" specifications (arc coefficient values) that are alike, and the faces (or other objects) could be distinguished from one another.

        Once reduced to a serial number code, a face or other object becomes adapted to an extremely wide spectrum of classification and searching tasks.     I suggest that patterns of classification (i.e.,"trees") can be searched, and can result in patterns involving an asymptotically large class of qualitative generalizations.    Within some specified pattern of classification, quantitative patterns of generalization can also be done, involving shape and/or quantity.   Ranges of numbers or symbols, rather than exact matches, can be searched (in a pattern called "fuzzy logic").   This range searching capability greatly widens the system's ability to generalize.

     The serial number format set out here can work for a substantially unlimited range of qualitative and quantitative generalizations, including logically programmed categorization sequences that mix specificity and generality in a manner familiar to database searchers (and knowledgeable recipients of junk mail).    Limitations of this sort of system are also interesting.  A database system can be superbly "intelligent" in the manipulation of a set of inputs that fit its database classification format.   The same database system may be much less efficient, or totally incapable, in the face of a problem that does not fit its classification system.   These strengths and weaknesses are analogous to strengths and weaknesses in human and animal behavior⁽¹⁶⁾.

CASE 9. DATABASE MANIPULATIONS IN ANALOGY TO LANGUAGE

     Computer "languages" and database "languages" are called languages for good reason (Simon etc).   An image processing system of database form has particularly close analogies to language.   Abstracted database forms (i.e., "trees") will act as nouns.   Many data forms will act as noun modifiers.   Positional information will need a positional notation that acts as prepositions act.   The verb "to be" will be implicit in the system.   Other verbs will come in as soon as action becomes expressible.   With verbs will come verb modifiers.   Any such system will have a grammar.   Once the processing of geometry is reduced to the class of the serial numbers, language-like systems are logically close.

      A system with these characteristics has plain similarities to human language.    However, the differences between human language and a "general vertebrate code" will be substantial, too.    The brain is a massively parallel system and must often manipulate data structures that carry much more quantitative information than human language can handle.   For example, human language could not adequately convey the huge number of inherently quantitative and simultaneous instructions that an animal would need to control its muscles.   Nor will language serve adequately to encode, regenerate, or manipulate images.   A much more parallel code system with much higher quantitative capabilities would be required for muscular control and many other kinds of computation and control an animal must do.   Human language can be conceptualized as a specialized code that interfaces with lower levels of general vertebrate codes through abstracted systems of subroutines.   Human language is constrained to sequential function for both input and output.   Moreover, human language works with highly abstracted "objects" that have been almost entirely stripped of their quantitative aspect.   Human language is therefore well adapted for high level classificatory and manipulative tasks where task validity is insensitive to questions of quantity.   Human language also has the immense advantage that it permits groups of human beings to communicate with each other in detail.

     Animal function requires "general vertebrate codes" that are better than human language in some ways, but worse in others.    I suggest that simple forms of these codes must have worked in many of the animals, some of them early arthropods, preserved in the Cambrian Era's Burgess Shale, and that these codes and code systems have been part of the neurology of life since that time.

    When an encoding is found that is adaptable to database manipulations, the evolution of a real language is very near.   Database systems capable of classification and image manipulations are languages in the computer sense, and operate in close analogy with human languages in some striking and basic ways.

COULD THESE SYSTEMS BE BIOLOGICAL?:

      Are the systems set out here biologically real and significant in mammals and other animals?    As of now, the point cannot be proved, though it seems likely on functional grounds.      It seems worthwhile to review these functional grounds.    

A new class of code-using neural network systems has been shown.

     Lateral inhibition and lateral excitation networks are primary components of these systems: if calibrated, these widely occurring neural forms can encode or decode polynomial functions, and are electrochemical analogs of Babbage's Difference Engine #2.   These systems can do many jobs involving geometrical manipulation, image recognition, image processing, motion prediction, change and motion sensing, visual orientation, motor control, and symbol processing.  The systems seem capable of one trial learning.  These systems seem capable enough and fast enough for many of the jobs that brains do.

    These systems form a link between "connectionist" and "symbolic" neural theory. The arrays shown, in combination with "connectionist" arrays, can form facile symbol and math manipulating systems.

    These systems make and use codes. The codes for these systems encode curves or images (linked combinations of curves) as polynomial arc system "serial numbers."   Encoded curves or images can be recognized, reconstructed, and manipulated over a wide range of translations, rotations, scalings, and distortions.   Database-like constructions from these encodings are adapted to many kinds and degrees of qualitative and quantitative generalization.   Direct code developments would produce a language-like "general vertebrate code" with "word analogs" (nouns, adjectives, prepositions, and verbs) adapted for control, imagination, and scripting.

    I suggest that the structural and mathematical patterns set out here are biologically interesting, either directly or by way of analogy, because of what they can do and because they are simple enough that their evolution is plausible.

1. Laughton, S.B. (1989) Introduction in PRINCIPLES OF SENSORY CODING AND PROCESSING, volume 146 of The Journal of Experimental Biology September.

2. . The word "array" will be used in a tripartite sense in this paper, with the biological sense emphasized and the engineering and mathematical senses implicit. The first sense is mathematical: these arrays and array systems are mathematically understood and have worked well on a computer. The second sense is technical: those skilled in the art of Very Large Scale Integrated (V.S.L.I) circuit design and other robot-related engineering arts should see that these "robotic array" systems could produce many animal-like characteristics in man-made robots, although they have not yet been built into working systems. The third sense is biological. These array systems are proposed as living "neural arrays" in vertebrates and the higher invertebrates. This third level is emphasized in this paper.

3. op. cit.

4. Shepherd, Gordon M. (1986) "Apical Dendritic Spines of Cortical Pyramidal Cells: Remarks on their possible roles in higher brain functions, including memory" in SYNAPSES, CIRCUITS, AND THE BEGINNINGS OF MEMORY Gary Lynch, ed, MIT Press, Cambridge.

5. Black, Ira B. (1986) "Molecular Memory Systems" in Lynch, Gary SYNAPSES, CIRCUITS, AND THE BEGINNINGS OF MEMORY MIT Press, Cambridge.

6. Newsome, William T., Britten, Kenneth H., and Movshon, J. Anthony (1989) "Neuronal Correlates of a Perceptual Decision" NATURE, vol 341, 7 Sept page 52.

7. Bromley, Allan G. (1982) "Introduction" in BABBAGE'S CALCULATING ENGINES (a collection of papers) Tomash Publishers, Los Angeles and San Francisco.

8. Babbage, Charles (1822) quoted by Cherfas, J. in Science, 7 June, 1991, page 1371.

9. Menabrea, L.F. (1842) 'Sketch of the Analytical Engine Invented by Charles Babbage, Esq." in BABBAGE'S CALCULATING ENGINES: A COLLECTION OF PAPERS Tomash Publishers, Los Angeles and San Francisco, 1982.

10. Boole, George (1860) THE CALCULUS OF FINITE DIFFERENCES 4th edition Chelsea Publishing Co. New York.

11. Shepard, Roger N. (1989) "Internal Representations of Conceptual Knowledge" in NEURAL CONNECTIONS, NEURAL COMPUTATION (L. Nadel, L.A.Cooper, P.Culicover, and R.M.Harnish, eds) MIT Press, Cambridge.

12. Kline, Stephen Jay (1965, 1984) SIMILITUDE AND APPROXIMATION THEORY McGraw Hill, New York.

13. Boole, George (1854) AN INVESTIGATION OF THE LAWS OF THOUGHT reprinted by Dover, New York.

14. Hofstadter, D.R. (1985) "Waking up from the Boolean Dream, of, subcognition as computation." In D.R. Hofstadter METAMAGICAL THEMAS, Basic Books, New York.

15. Smolensky, Paul (1989) "Connectionist Modelling: Neural Computation/ Mental Connections" in NEURAL CONNECTIONS, MENTAL COMPUTATION (L. Nadel, L.A.Cooper, P.Culicover, and R.M.Harnish, eds.) MIT Press.

16. J.S.Bruner and Leo Postman "On the Perception of Incongruity: A Paradigm" Journal of Personality, XVIII (1949) 206-23. Cited in T.S.Kuhn THE STRUCTURE OF SCIENTIFIC REVOLUTIONS op.cit. p 62-63