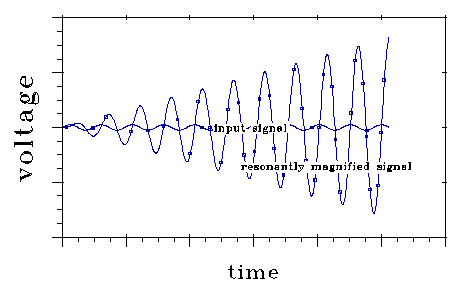
FIG AP3-1
Appendix 3: Some background on resonance
Electrical resonance can store up energy in an oscillation. Fig Ap3-1 shows how the voltage oscillation stored in a resonant system grows when it is driven at its resonant frequency (in magnifying phase.)

FIG AP3-1
If the dendritic spines of neurons are analyzed assuming the S-K transmission
equation, they will show such resonance. Resonant magnifications may be
very great, and bandwidths extremely narrow, as shown in the dendritic
spine resonance calculations graphed in Fig AP3-2:
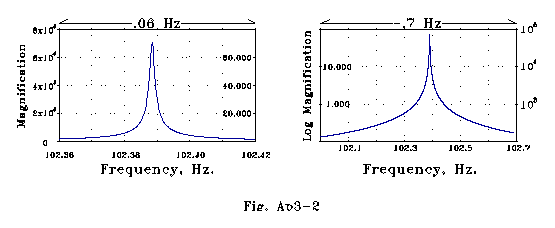
Resonant systems may all be described in wave propagation terms, and
many can also be treated in lumped (LRC) terms.
The International Dictionary of Applied Mathematics explains
inductance-resistance-capacitance (LRC) series resonance as follows. The
"coil" is a lumped inductance, the "condenser" is a
lumped capacitance, and "j" is the square root of -1.
. . . In an a-c circuit containing inductance and capacitance in series
... the impedance is given by
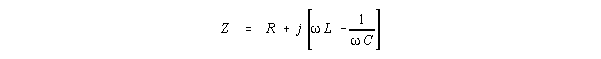
where R is the resistance, is 2 times the frequency, L is the inductance,
and C is the capacitance. It can be readily seen that at some frequency
the terms in the bracket will cancel each other, and the impedance will
equal the resistance alone. This condition, which gives a minimum impedance
(and thus a maximum current for a fixed impressed voltage) and unity power
factor is known as series resonance. Where the resistance is (relatively)
small the current may become quite large. As the voltage drop across the
condenser or coil is the product of the current and the impedance of that
particular unit, it may also become very large. The condition of resonance
may even give rise to a voltage across one of these units that is many
times the voltage across the whole circuit, being, in fact, Q times the
applied voltage for the condenser and nearly that for the coil. This is
possible since the drops across the coil and condenser are nearly 180 degrees
out of phase, and thus almost cancel one another, leaving a relatively
small total voltage across the circuit . . .(1)
A neural element according to K-R will have no inductance, L. There
is no LRC resonance under K-R. That same neural element according to S-K
may have very large inductance. For an LRC resonator, the resonant frequency,
o is:
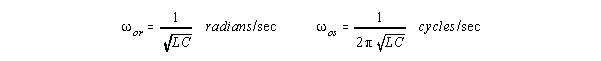
The resonant amplification factor, Q, achieved after time to
equilibrium(2), is:
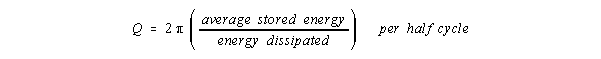
For an LRC resonator, Q is
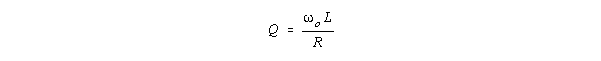
Bandwidth (the frequency difference between the half power points on
a resonance curve) is:
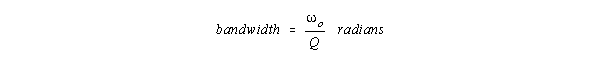
In addition to lumped (LRC) resonance, columns can also be resonant.
Columns (transmission lines) of 1/4 and 1/2 wavelength have been used as
resonators in musical instruments for many centuries. More recently, column
resonance has been used with precision in the radar and communication fields.
Well terminated lengths of neural passage that are sharply open (short
circuited) at both ends are resonant when there length is exactly 1/4 of
. For column length lc:
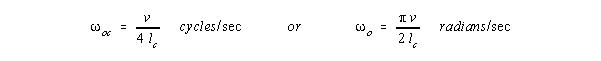
and integer multiples of o. A well terminated length of neural
passage that sharply closed on one end will be resonant at

and integer multiples of these frequencies.
Consider a neural (dendritic) passage in terms of its defining variables,
d, conductor diameter, = membrane thickness, = membrane dielectric
constant and = axolemma conductivity.
Assuming S-K, conduction velocity in small neural lines (above a very
low threshold frequency) is constant. v is:
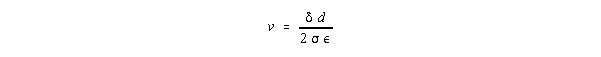
For a 1/4 wave resonant column of length lc:
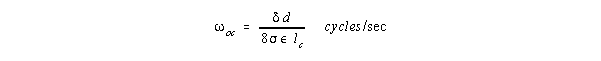 .
.
Q of the column resonator will be inverse with attenuation per wavelength
.
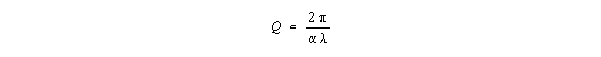
According to K-R, attenuation per wavelength is enormous, Q's are very
small, and resonant energy storage does not occur. According to S-K, attenuation
per wavelength can be very small, Q's can be in the thousands or tens of
thousands, and resonant energy storage can be important. Substituting the
neural formula for attenuation per wavelength, , for a well terminated
passage (having ends with 100% positive or negative reflection) Q becomes:

Note that Q increases with o. Column resonator bandwidth
in terms of o, , , and is
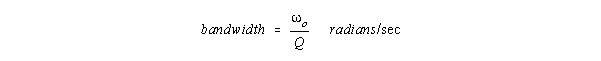
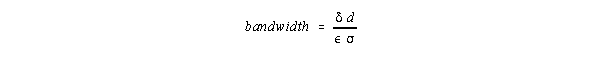
Column resonators magnify and store repeating WAVEFORMS that fit as standing
waves within them. In contrast, an LRC resonator stores a sine wave.
For spines, LRC mode Q's in the tens of thousands are possible on the
assumption of S-K. Assuming K-R, there is no LRC resonance. Similarly large
Q's are possible in column resonant mode assuming S-K. There is no column
resonance under K-R.
1. The International Dictionary of Applied Mathematics D.Van Nostrand Company, Princeton, Toronto, New York, London 1960