Appendix 1: Derivation of a finite increment equation from a coupled physical model, showing combined effect terms.

Most mathematical models of physical circumstances start by matching one or more differential equations from a handbook with a physical case. Thereafter, analysis is carried out according to the rules of abstract mathematics. In this usual procedure, the differential equation is not derived from a physical model, but is applied to that model and taken as an operationally perfect or good enough match.

However, the differential equations themselves are sometimes inferred directly from physical models in a step by step way from a sketch-model. This process is called "derivation," and is taught in engineering schools.

To derive a differential equation from a physical model

       construct a finite scale model that sets out the laws and geometry to be represented;
 
       then derive (one or more) finite increment equation(s) that map that finite model.

       After a finite increment equation that represents our model has been defined, we may
       pass that finite equation to the infinitesimal limit to yield a differential equation.

Equation definition can take special attention if our finite model includes coupled effects. In such a case, two equations are implicitly defined in terms of each other.

One of the simplest and most important examples is current change and voltage change along a length of conductive line (such as a wire or a length of neural tube.) Current drops i are coupled to voltage and voltage drops according to logic like the following:

i over the interval is a function of v at x and x+x
     which is a function of i at x and x+x
             which is a function of v at x and x+x
                       which is a function of i at x and x+x

                                             and so on

Voltage drops are coupled to current and current drops in the same nested way.

We have to be able to represent the coupled effects that occur correctly at finite scales, before we can take the limit of those terms, at successively smaller finite scales, to the infinitesimal limit.

Fig. 1 shows a conducting line that could be neural conductor.

v = voltage    i = current    x = position along the line    alpha= arbitrary length interval
R = resistance/length          L=electromagnetic inductance/length
G= membrane leakage conductance/length          C=capacitance/length


Fig. 1 shows an arbitrarily chosen length , of arbitrary magnitude, which we will call  deltax.

R, L, G, and C are natural law operators (Appendix 2 .) They represent physical laws, and are defined as the ratio of one measurable to another under particular measurement circumstances. The natural law operators, which implicitly represent much measurement detail, are our interface between the detailed measurement procedures of physical reality and abstract equation representations of physical circumstances. Natural law operators are justified by inductive generalization, not axiomatic proof. We have no provable reason to think R, L, G, and C have exactly the properties of numbers. In the derivation below, we'll operate on terms including the symbols R, L, G, and C in the usual algebraic way, stopping short of algebraically simplifying the terms. We'll not interpret these terms numerically or physically here in appendix 1, leaving that for Appendix 2 .

To derive line differential equations in dv/dx and di/dx, we first need finite difference equations, dv/dx and di/dx. For the finite equations, we'll be writing out terms that have usually been understood to exist, but that have been called infinitesimal and neglected. Let's consider the coupled effects physically.

        Voltage drop over deltax depends on current. Current over length deltax varies if charge carriers are         stored or  discharged in capacitance over the interval deltax. The capacitive effect will depend on dv/dt.         Current over deltax  will also be lost from membrane leakage over delatx. That loss will depend on v.         Voltage drop depends not only  on current, through R, and L, but also depends on interactions between         voltage and G and between dv/dt  and C.

In an exactly symmetric way

         Current drop over deltax depends on voltage. Voltage over length deltax varies with inductive reactance,           L di/dt. Voltage over deltax will also be lost from interaction between resistance and current, Ri. Current           drop depends not only on voltage, through G and C, but also depends on interactions between current           and R, and between di/dt and L.

The idea that di/dt depends ONLY on G and C neglects effects that act over deltax. The idea that dv/dt depends ONLY on R and L neglects crosseffects over deltax.

Let's derive voltage and current equations that include crosseffects. We'll write our voltage and current functions as v(x,t) and i(x,t).   We assume homogeneity and symmetry for our conductor.   We assume that, for the small lengths of interest, the average voltage (average current) across the interval deltax is the average value of voltage (current) at the endpoints of the interval deltax.

Writing down voltage change as a function of the natural law operators and variables that directly affect voltage, and centering our interval at x, so that our interval goes from x- deltax/2 to x+deltax/2, we have:

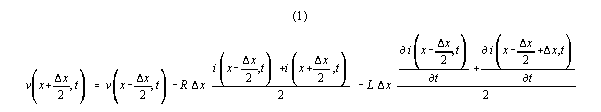
The current change equation is isomorphic:

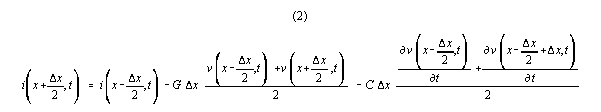
Note that equation (1) includes i(x+deltax/2,t) and its time derivative. i(x+deltax/2,t) is defined by equation (2).

Equation (2) includes v(x+deltax/2,t) and its derivative. v(x+deltax/2,t) is defined by equation (1).

Each of these equations requires the other for full specification: each contains the other.

If the cross-substitutions implicit in these equations are explicitly made, each of the resulting equations will also contain the other. So will the next generation of substituted equations, and the next, and so on. This is an endless regress. Each substitution introduces new functions with the argument (x+deltax/2), and so there is a continuing need for more substitutions. To achieve closure, one needs a truncating approximation. Expression of current, voltage, and their time derivatives at x, the midpoint of the interval, truncates the series.

Let's proceed with these substitutions, associating symbols without interpreting them numerically or physically. For example

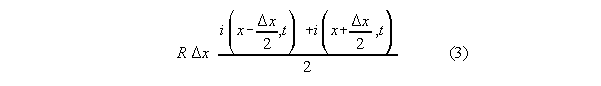
is

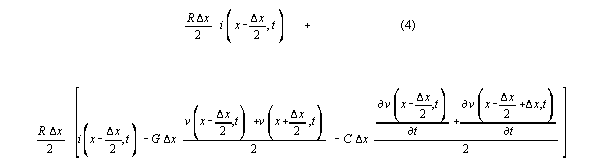
which expands algebraically to

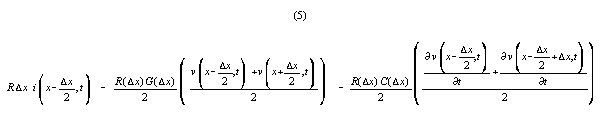
These terms would be simpler if voltage averages and derivative averages were taken at the interval midpoint, x, as follows:

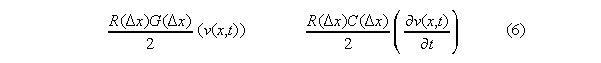
How may terms like those of (6) be interpreted, physically and numerically, at finite scale? In these expressions, two natural law operators are EACH associated with the SAME interval of length. Do the lengths multiply? On what authority do we say that the lengths multiply? If the lengths do multiply, what does this represent physically? Does the multiplication make numerical sense, and is that multiplication consistent with tests the expression must pass? It turns out that if we apply standard arithmetical rules to these crossterms, we are led to mathematical and physical inconsistencies. (Appendix 2 )

The equation below shows voltage change over an interval of length deltax, divided by the length deltax to produce a gradient form analogous to a derivative. Terms derived from three stages of cross substitution are shown. Symbols are grouped together and algebraically simplified up to the point where the meaning of further algebraic simplification of relations in the dimensional parameters R, L, G, C, and deltax becomes unclear. Expresssions in curly brackets are NOT YET DEFINED.

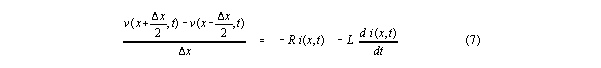
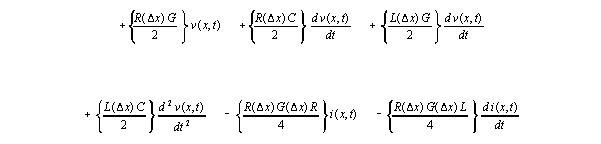
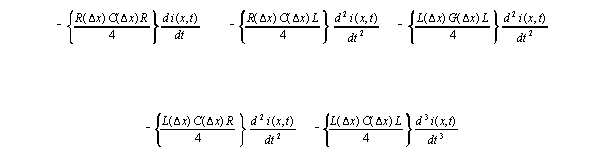
The current gradient equation over the same interval is isomorphic to 7 with swapping of v for i, R for G, and L for C.

Whenever coupled physical effects act over an interval of space, combined effect terms are to be expected. Rules for their interpretation must be found. Those rules are beyond the authority of the axioms of pure mathematics, but consistent rules for interpreting these expressions can be inferred from mathematical experiments. (Appendix 2 )

Combined effect terms such as those shown here are seldom derived, because they are thought to always vanish in the limit. However, that interpretation involves basic inconsistencies (Appendix 2). Expressions such as those in the curly brackets, interpreted in a consistent way, are finite, and yield finite terms in differential equations. Often such combined effect terms are negligible, but sometimes they are important.