MODELLING OF PHYSICAL SYSTEMS ACCORDING TO MAXWELL'S FIRST METHOD

                                                                                       by M. Robert Showalter⁽¹⁾ and Stephen J. Kline⁽²⁾

        Logically rigorous attempts to write out models that reflect physically detailed circumstances have sometimes been blocked by undefined crossterms.      Physically arbitrary assumptions have long been accepted to avoid the difficulty.    Examples of these undefined crossterms are shown, and a definition procedure for them is set out so that more physical modelling procedures leading to abstract equations become possible.    An electrical transmission line model is used as the example.    Depending on the size of the parameters in the equation, the crossterms can be operationally indistiguishable from 0, or dominantly large.

        The jump between a physical system model, defined in terms of drawings, measurement procedures and other detail, and the abstract mathematical representation of it remains a partly mysterious one.     Nonscientists and smart students find this jump hard to follow, and hard to trust, generation after generation.   Scientists, by and large, take the jump on faith.  Korzibski's dictum is much quoted.

"The map [system representation, or sysrep] is not the territory [system]."

       However, in formal systems, such as mathematics, the system and the sysrep are identical by construction.   In such systems, the map is the territory⁽³⁾."   This is a reason for residual caution about our formal models. At a basic level, they are not self cleansing.    Experience provides other reasons for caution.    Mathematical modelling of physical systems has produced many triumphs, but also some disappointments.    For example, mathematical modelers of neural systems have not explained the information processing that we know brains do.   One reason, we think, it that the effective inductance of the presently accepted passive neural conduction equation is often too low by more than 10¹⁰ : 1⁽⁴⁾

. People doing theoretical work all through the pure and practical sciences have other difficulties, often unpublished, that provide residual reasons to doubt that our mathematical modelling procedures are always right. George Johnson⁽⁵⁾ says that

" Scientists must constantly remind themselves that the map is not the territory, that the models might not be capturing the essence of the problem, and that the assumptions built into a simulation might be wrong⁽⁶⁾. "

       We agree.     We've found Johnson's point directly applicable to mathematical modelling. We have had difficulty deriving valid modelling systems of coupled differential equations by conventional means, starting from finite increment equations.   Cases where we have failed to get good results by the standard means have included a piston ring⁽⁷⁾ design model and the passive neural conduction equation.   We have been re-examining the fit between formal mathematical mapping and the physical territory, and examining assumptions built into that mapping.   We found ourselves retracing ground first covered by James Clerk Maxwell.   We've found an error that we believe Maxwell may have suspected.   When that error is corrected, some terms now called infinitesimal (or infinite) are finite.   The error is very often entirely unimportant.   But it can have devastating effects in some cases, including cases important to an understanding of the brain.

        This paper shows the error, and shows how it may be fixed, proceeding from Maxwell's perspective, which might, today, be called a "philosophical" perspective.    It presents our fix, but does not prove that fix rigorously. Companion papers deal with the same subject matter from other perspectives.

     One paper shows that the error comes from an difference between measurable spaces and the abstract domain of the algebra, requiring an arithmetical restriction on our use of the dimensional parameters we use in our physical models, so that these models can be consistently and correctly mapped into the domain of the algebra⁽⁸⁾.

A second paper shows how some of our limiting arguments, that involve dimensional parameters, are false⁽⁹⁾;

A third paper shows by numerical example that the new interpretation of terms can be significant or insignificant depending on the numerical size of the dimensional parameters involved⁽¹⁰⁾.

Here is James Clerk Maxwell, writing a year before his death⁽¹¹⁾:

"There are two methods of interpreting the equations relating to geometry and the other concrete sciences.

"We may regard the symbols which occur as of themselves denoting lines, masses, times &c; or we may consider each symbol as denoting only the numerical value of the corresponding quantity, the concrete unit to which it occurs being tacitly understood.


"If we adopt the first method we shall often have difficulty in interpreting terms which make their appearance during our calculations.    We shall therefore consider all the written symbols as mere numerical quantities, and therefore subject to all the operations of arithmetic during the process of calculation.   But in the original equations and the final equations, in which every term has to be interpreted in its physical sense, we must convert every numerical expression into a concrete quantity by multiplying it by the unit of that kind of quantity."

      According to the first, more literal method Maxwell cites, we have "difficulty" interpreting some (cross effect) terms, indeed we cannot interpret them at all.    We are stopped. THEREFORE we make a plausible assumption. We make that assumption along with Maxwell, giants before him (Newton, LaPlace, LaGuerre, and Fourier) and workers since.   We decide to act AS IF our physical quantity representing symbols may be abstracted into simple numbers in our intermediate calculations. This assumption has produced equations that fit experiment innumerable times. But it remains a pragmatic assumption with no logically rigorous basis at all.

On Maxwell's first assumption, we have terms that are difficult (impossible) to interpret.

On Maxwell's second assumption, these terms fit readily into our calculus apparatus, and can quite often be "shown" by a limiting argument to be infinitesimal or infinite.

         The second assumption may therefore be shown wrong mathematically by finding an inconsistency in the arithmetical usages it assumes.    We have found such an inconsistency⁽¹²⁾.   The second assumption may also be shown wrong empirically by data showing that it calls finite terms infinitesimal, or calls finite terms infinities.   As described below, neural data indicates that effective inductance is many billions of times greater than that predicted by a conduction equation derived by Maxwell's second method.    Also, calculations according to Maxwell's second method that accounted for the dielectric capacitance of a conductive line calculated an infinite line capacitance, and hence a zero velocity of conduction.    That infinity has always been ignored on practical grounds.    By measuring conduction velocities in nearly pure water, velocities that are thousands of times less than the speed of light, one finds that the "infinite" dielectric capacitance of the conductive water medium is finite and consistent with the calculation procedure set out here (Showalter, in preparation) according to Maxwell's first method.

We have found that by adding a type limitation to the dimensional parameters we can interpret the kind of terms Maxwell calls "difficult." When this is done, Maxwell's first method becomes operational and new terms, now thought to be infinitesimal or infinite, are finite.

BIOLOGICAL MOTIVATION:

       The Kelvin-Rall, (K-R), equation is the standard electrical line conduction equation stripped of terms in electromagnetic inductance.   Reasons to doubt K-R have been accumulating, and are reviewed elsewhere⁽¹³⁾. The coherent propagation of action potentials seems inconsistent under K-R, particularly if channel populations are heterogeneous or sparse.   K-R seems a poor fit to observations concerning neural synchrony.   K-R predicts that neurons are slower than they are.   Under K-R, the low dissipation conduction observed in dendrites requires very special and demanding assumptions about channel distribution and behavior.   To us, the most compelling reason to doubt K-R is the EEG and MEG data of David Regan⁽¹⁴⁾ .

        Regan used the zoom FFT technique on electroencephalography and magnetoencephalography data.    He showed peaks organized in the integer multiple sums and differences characteristic of resonance.   The EEG and MEG data measured population behavior over a significant volume of brain.   Even so these integrated peak bandwidths were very tight, less than .002 Hz.   We were led to conclude that brain was an assembly including large populations of very high Q resonant structures coupled by the waves that the EEG was measuring.   Consulting anatomy, we had to assume that either short dendritic sections or dendritic spines were the resonant elements.   Regan's data, without which we would not have persevered, implied that the effective inductance predicted by the presently accepted Kelvin-Rall equation was too small by enormous factors (in the range of 10¹⁰-10¹⁸:1 for various cases.)   These same large factors fit action potential behavior.   We had these good reasons to question the derivation of Kelvin-Rall, that followed the "second method" cited by Maxwell.

Crossterms in derivation of coupled equations from models

This paper shows how the "difficult to interpret" crossterms come about in the derivation of electrical line equations from a physical model set out interpreting "the symbols which occur as of themselves denoting lines, masses, times &c."

To derive a differential equation from a physical model in classical physics, we argue as follows, and generally do so without formal distinction between Maxwell's first and second methods:

1. We construct a model (including a sketch, and any necessary information) at a finite scale that represents the laws and geometry in question.


2. We derive finite increment equation(s) that map(s) the finite model.


3. We infer the form of the finite increment equation at smaller and smaller scales, until it is defined at point (differential) scale. THE EQUATION AT DIFFERENTIALLY SMALL INCREMENT SCALE IS THE DIFFERENTIAL EQUATION⁽¹⁵⁾

.

       Let's proceed to infer a finite increment equation for electrical transmission along a line, a case that is inherently coupled.    We proceed according to Maxwell's first method, using symbols and arithmetical operations to represent a physical situation, not just manipulating abstract and disembodied number-symbols.

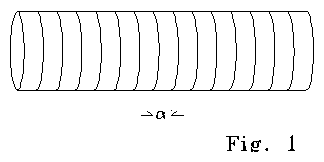
Fig. 1 shows a neural conductor (axon or dendrite considered as a transmission line). A tubular membrane is filled with and surrounded by an ionic fluid. The fluid inside the tube carries current (and signal) and has resistance R and electromagnetic inductance L per unit length. The outer fluid is grounded. The membrane separating these conducting fluids has capacitance and leakage conductance per unit area. We speak of the following variables and parameters:

v = voltage                     i = current
x = position along the line                       delta x= arbitrary length interval
R = resistance/length                          L=electromagnetic inductance/length
G= membrane conductance/length                C=capacitance/length

Fig. 1 shows an arbitrarily chosen length, alpha, which we will call  delta x because that is commonly done.   Length increment alpha, which we call delta x,  is picked from other indistinguishable lengths. (For consistency, the length of is a number delta times the unit of measure used in the calculation in the x direction (meters, cm, or whatever).)   We are giving length alpha a two-symbol name that includes a separate number.  Other entities that have numerical values in our calculations are denoted as single symbols, and do not have separate numerical symbols (such as delta) associated with them.

    We need finite difference equations that define, delta v/delta x and delta i/delta x.   For the finite equations, we'll be writing out terms that have usually been understood to exist, but that have been called infinitesimal (based on Maxwell's second method) and neglected.

Because voltage drop over a length alpha depends on current, and current over length alpha partly depends on charge carriers stored in capacitance or lost through membrane leakage over alpha, we know that delta v/delta x for delta x= alpha  must partly depend on effects including C and G over length alpha=delta x

and

Because current drop over length alpha depends on voltage change over alpha, and voltage change over alpha partly depends on R and L, we know that delta i/delta x  for delta x=alpha  must partly depend on effects of R and L over length alpha=delta x.

From such interactions, it follows that:

delta i over the interval is a function of v at x and x+delta x
       which is a function of i at x and x + delta x
                which is a function of v at x and x + delta x
                    which is a function of i at x and x+delta x
                             and so on
                                   and so on .    .    .     .

In current practice, when we derive a differential equation from such a coupled relation, we say:

i over the interval is a function of v at x and x+delta x
                                               (and nothing more.)

       The truncation implied in the words "and nothing more" follows from the second method Maxwell cites, because the crosstems are infinitesimal under that assumption.    The truncation does not follow from Maxwell's first method.

        Let's derive voltage and current equations that include crossterms.    We'll see why the crossterms cause us "difficulty in interpretation."    We'll write our voltage and current functions as v(x,t) and i(x,t).    We're assuming homogeneity and symmetry for our conductor.   We assume that, for small enough lengths delta x, the average voltage (current) across the interval from x to x+delta x is the average of the voltage (current) at x and at x+delta x.

Writing down voltage change as a function of the dimensional parameters and variables that directly affect voltage, we have.

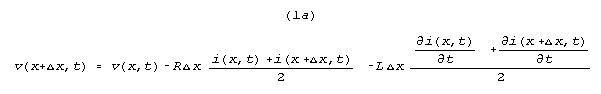
Writing down current change as a function of the dimensional  parameters and variables that directly affect current, we have.

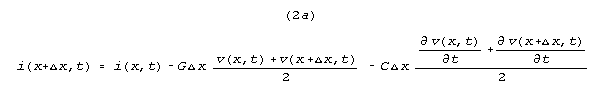
We may equally well rewrite (1a) and 2a) going from points x-delta x to x+delta x, so that the interval is centered at x.

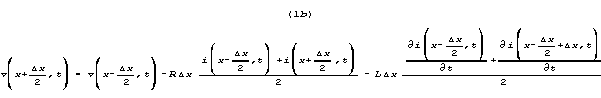
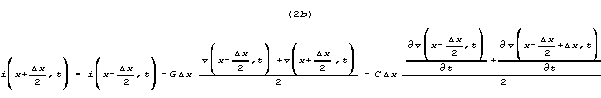
Note that equation (1b) includes i(x+x/2) and its time derivative. i(x+x/2) is defined by equation (2b). Equation (2b) includes v(x+x/2) and its derivative. v(x+x/2) is defined by equation (1b). Each of these equations requires the other for full specification: each contains the other.

If the cross-substitutions specified implicitly are explicitly made, the resulting equations will also each contain the other. So will the generation of equations following, and the next, and so on. This is an endless regress. Each substitution introduces new functions with the argument (x+x/2), and so there is a continuing need for more substitutions. To achieve closure, one needs a truncating approximation position of x, for current, voltage, and their time derivatives.

We can proceed with these substitutions, associating symbols without interpreting them numerically or physically. For example

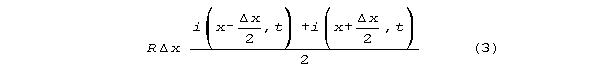
is

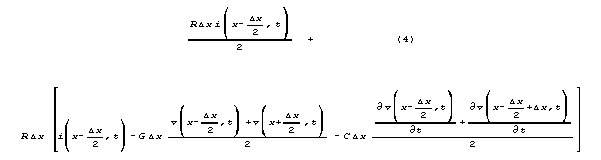
which expands algebraically to

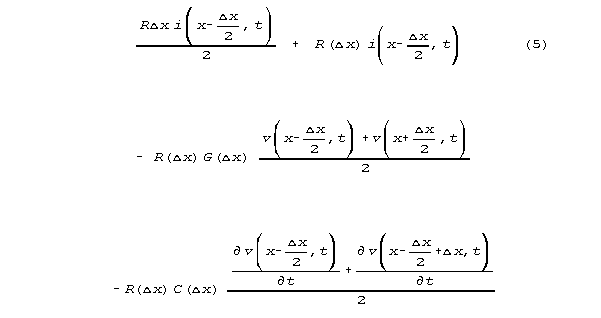
These terms would be simpler if voltages and derivatives of voltages were taken at the interval midpoint, x. But even so simplified, it is terms of this kind that are "difficult to interpret" in Maxwell's sense. (Maxwell was an industrious analyst living in an analytically competitive world, and when he wrote "difficult to interpret" he meant operationally impossible.)

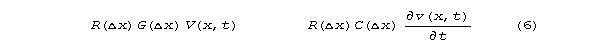
We are not yet concerned with the size of these terms. That is a matter of arithmetic. We are concerned with their existance. If one wishes to speak of expressions like those of (6), what do they mean for finite when the symbols are considered to stand for fully physical things, or complete models of physical things, subject to the detailed physical rules that stand behind the model? How do you interpret them with a sketch interpreted by measurement procedure? The second author, who has written a standard book on dimensional analysis⁽¹⁶⁾ could not interpret these expressions. In discussions with mathematicians, engineers, and scientists, the first author was not (for three years) able to find anyone who was confident of the meaning of these kinds of expressions at finite scales (or, as a matter of logic, when length was reduced to an arbitrarily small value in a limiting argument.) Maxwell seems to have had the same difficulty. The equations below shows voltage change over an interval of length x, centered about the point of position x, for three stages of cross substitution. Symbols are grouped together and algebraically simplified up to the point where the meaning of further algebraic simplification of relations in the dimensional parameters R, L, G, C, and x becomes unclear.

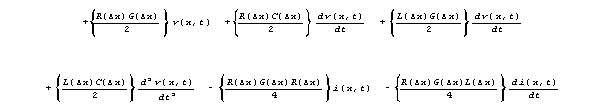
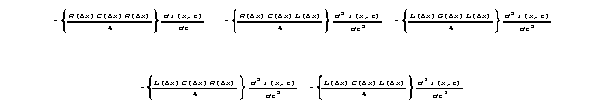
Again, we are concerned with the formal meaning of these terms, and not yet with their size. Their size depends on the values of R, L, G, and C that apply to a particular physical case.

The equation for i(x+x/2,t)-i(x-x/2,t) is isomorphic to 7a with swapping of v for i, R for G, and L for C.

Here are the terms in 7a where we encounter Maxwell's "difficulty."

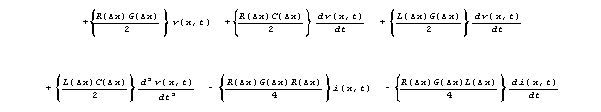
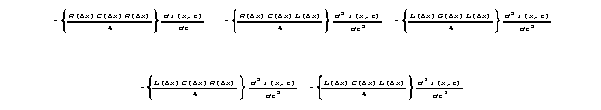
These "difficult" terms all represent combined physical effects that integrate together over a length. When we interpreted these terms by scaling and sketching arguments, we encountered questions of definition, but it always appeared that the magnitude of these cross effects must be CONSTANT per unit length. However, in currently standard analysis, the combined effects represented in the crossproducts above vanish, because according to that analysis these same crossterms vary with length so that they vanish in the limit. For some time we were stalled about here, knowing that we had a contradiction, but not knowing how to resolve it.

Maxwell describes the standard assumption that avoids the difficulty in literal, dimensional, interpretation of these terms, and explains why he reluctantly accepted that assumption. His justification for this assumption is strange enough to bear repeating (and strange enough to help explain why some smart, careful students, who wish to carefully and redundantly trace decisive stages of logic as they learn them, can distrust mathematical modelling procedures, and can even refuse to learn and use them.) If we consider our physical symbols as representations of the fully dimensional things they stand as names for, and if we ask to make physical sense of some crossterms as physical entities, we find that we cannot interpret them at all⁽¹⁷⁾. We are stopped. THEREFORE we decide to act AS IF our physical quantity representing symbols are NO MORE than simple numbers in our intermediate calculations. (That is, we classify the issues that involve the details of measurement and measurement derived definition out of existance in the map we choose to use.) Efficient though this assumption has often been, the assumption has no logically rigorous basis at all. This is a mapping logic that teachers typically do

not even attempt to teach. Instead, it is imposed. Students who

rebel here are lost to the more quantitative kinds of science.

The assumption we call "Maxwell's second method" is so convenient and has become so reflexive that we do not think to suspect it. Once the assumption is made, dismissal of the "difficult terms" above follows directly. We "consider all the written symbols as mere numerical quantities, and therefore subject to all the operations of arithmetic during the process of calculation." Our "difficult" terms may then be analyzed by a standard limiting argument. Taking the limit as length x approaches 0, these terms vanish (or become infinite). This limiting argument is longstanding and indeed reflexive practice for working analysts. Some of the best such analysts, long accustomed to standard practice, may find it hard to even think about the possibility that "the written symbols" . . . might NOT be "subject to all the operations of arithmetic" in a map that really fit the natural territory being described. We understand these conceptual difficulties. We had them.

Even so, we also had reasons to question Maxwell's second (and standard) method. Empirical concerns in neural modelling have been described before and elsewhere⁽¹⁸⁾. We also had problems at the theoretical interface of physical modelling and analysis. Looking at crossterms in coupled equations like 7a, we had some procedural uncertainties but we could show, by sketch-modelling, that the crossterms must be finite (and might be large) at finite scales. But there was an inconsistency. A coupled equation like 7a, expressed at length x, could be reduced to a differential equation. That differential equation could then be integrated up to scale x. The integrated value would be different from the value of the finite increment equation it came from at scale x, by the value of the (finite) crossterms. We found that this could be a numerically large disparity and contradiction.

We have found that the dimensional parameters, such as R, L, G, C are not "just dimensional numbers," and are not "subject to all the operations of arithmetic" in the expected way. Operation with these dimensional parameters is subject to an additional, easy, but new rule.

To see our reasoning in connection to Maxwell's statements, let's rewrite 7a, substituting the symbol "length" for x.

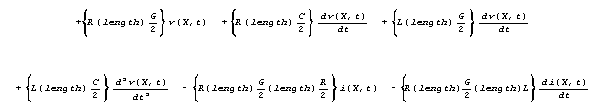
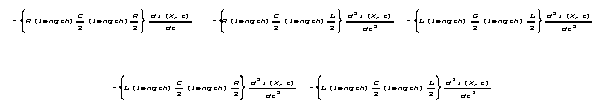
Now, suppose we shrink our length interval to a point. (Not a very short interval, but a point.) One may have questions about what the notion of a point means, but the length (or area, or volume) of a point is not some finite value. A point is of limitlessly small extent, not some numerically specifiable extent. Even so, point values of R, L, G, C, i, v, and t are all numerically well defined and familiar.

To advance our argument, let's use the expression (length)_p for "length at a point" without yet defining what that will have to mean.

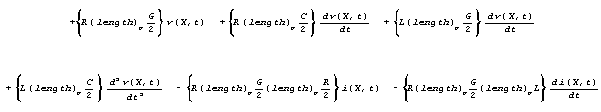
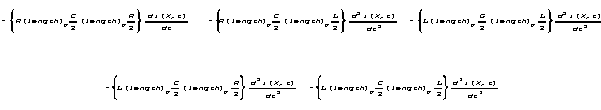
The notion of a "point" is associated with conceptual difficulties, some of them much involved with the history of mathematical inquiry over centuries⁽¹⁹⁾. An ordinary dictionary may devote several columns to the word "point"⁽²⁰⁾. A mathematical dictionary may refrain from defining "point" at all⁽²¹⁾. Even so, the usual mathematical idea of a point is a position in some defined space, where the position is so sharply defined that it has position but not extent. According to this idea, a point has zero length, zero area, zero volume, and a point in time has zero temporal extent. The notions of "length at a point" or "volume at a point" or "area at a point" are necessarily abstractions and generalizations of length, volume, and area over finite extents. These are necessary notions, that are embedded in our usage of point values of many quantities such as the following.

pressure, density, resistance, inductance, pressure, shear stress, viscosity, thermal conductivity

For example, pressure at a point includes implicitly the notion of area at a point. Density at a point, which is mass per unit volume at a point, implicitly includes the notion of volume at a point. Resistance per unit length at a point implicitly requires a notion of length at a point. However, arithmetically clear statements about what must be meant by "length at a point," "area at a point," "volume at a point," or "a point in time" have not been available. Perhaps it is better to say that arithmetically clear statments about what must be meant by "the property of length at a point," "the property of area at a point," "the property of volume at a point," and "the property of time at a point in time" have been unavailable.

We have found that the dimensional parameters⁽²²⁾, such as R, L, G, C are not "just dimensional numbers" and are not "subject to all the operations of arithmetic" that Maxwell's second method requires. For instance, the following expressions, taken from 7a, are not arithmetically consistent entities as now interpreted:

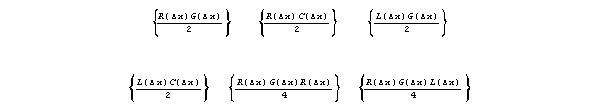
These expressions, evaluated in different units, or according to

different patterns that should be arithmetically acceptable, yield contradictory results^{(23) (24)}. We have been applying our ordinary arithmetic rules to entities like this, that are subject to particular arithmetical restrictions, not knowing of the restrictions. Doing so, we've been persuading each other by limiting arguments that are incorrect⁽²⁵⁾. The dimensional parameters, such as R, L, G, and C, are subject to an additional rule that ordinary numbers do not have. Here is the rule, applied to derivation of differential equations from finite increment physical models⁽²⁶⁾:

When we represent a finite increment physical SYSTEM ("Maxwell's first method represented system") in the form of a differential equation (defined at a POINT in space and time) we must put ALL the variables and increments into POINT FORM - it is not valid to have all the quantities except the increments in point form, with the increments in extensive form. The point forms of spatial quantities and time (expressed here in cm and second units) are:

length at a point: (1 cm)_p area at a point: (1 cm²)_p

volume a a point: (1 cm³)_p a point in time: (1 second)_p

with the UNITS of length, area, volume, and time

and

the NUMERICAL VALUES of 1 = length/length, 1= area/area

1 = volume/volume, and 1= time/time respectively

With ALL the variables and increments in our equation representation set out in point form, algebraic simplification yields a differential equation that validly represents our system.

This new rule can be operationally identical to our current limiting procedures, or radically different from those procedures, depending on the numerical size of the dimensional parameters we happen to be dealing with in a particular physical case.

Once our equations are represented in this way, we can do valid arithmetic on every term (neglecting the subscript p that is only a marker.) Let's rewrite 7b with " (1 cm)_p substituted for "length_p". We lack the space to write out the numerical and unit parts of R, L, G and C, which are well understood.

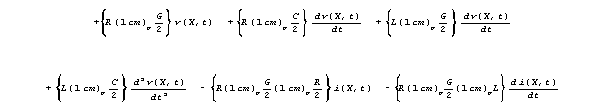
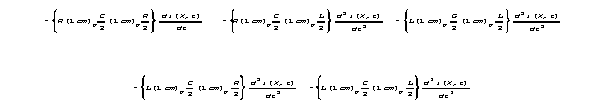
When we separate R, L, G and C into numerical parts (R_n, L_n, C_n, and G_n) that are algebraically simplified together, and unit groups that are algebraically simplified together, we can do valid arithmetic on equation 7c. The result, set out in semi-arbitrary voltage-unit, charge-unit, cm, time-unit system (v-Q-cm-t units) is:

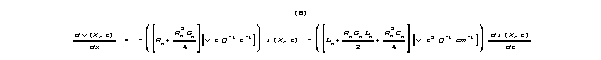
The analogous di/dx equation is

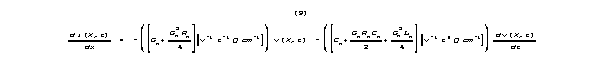
These differential equations, when integrated to length x, reconstruct the values that apply to that length x, with no lost terms, as they should. Every term in these differential equations passes the loop test set out in a companion paper⁽²⁷⁾. We may map these differential equations symbol-for-symbol into corresponding partial differential equations. We may map these differential (or corresponding partial differential) equations symbol-for-symbol into the domain of the algebra. These equations are different equations from the Kelvin-Rall equations, which lack all the terms below the first line of 7a.

With this procedure, the first method Maxwell cites becomes operational. Symbols can be interpreted as explicitly physical quantities, algebraically manipulated, and then, without assumption, mapped into abstract mathematical equations. Dimensional entities, the dimensional parameters, involve a procedural restriction that effects the algebraic simplification of crossterms. Equations that result from a proper algebraic simplification of such terms can then be mapped into the domain of the algebra, and used without any further restriction on our familiar arithmetical usages.

For MOST purposes, this new derivation is just like the old one. The new terms produced are finite, but they are usually too small to consider, even in the most accurate modelling work. However, for some purposes, the new terms are important. The relative and absolute importance of the terms depends on the numerical values that the dimensional parameters R, L, G, and C happen to have. These relative and absolute importances do not change when particular values of R, L, G, and C are changed from one unit system to another.

Let's consider our dv/dx equation

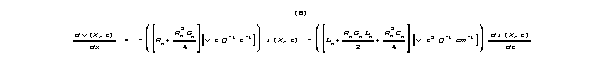
for a wire (or a neuron) and see how arithmetical logic determines the terms our modelling equations should include. We'll fill in numerical values for equation 8, for a wire, and for a neural line. For a 1 mm copper wire with ordinary insulation and placement, typical values of the dimensional parameters would be:

R = .14 x 10^-4 ohm/cm C = 3.14 x 10^-9 farads/cm

G = 3.14 x 10^-10 mho/cm L = 5 x 10^-9 henries/cm

and the equation 8 can be written as follows (with numerical values

of the symbolic terms written below the symbolic terms below.)

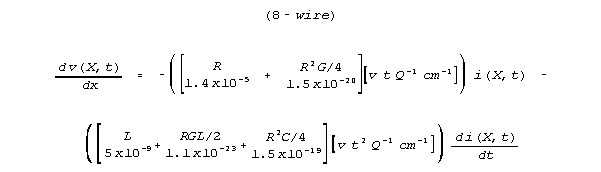
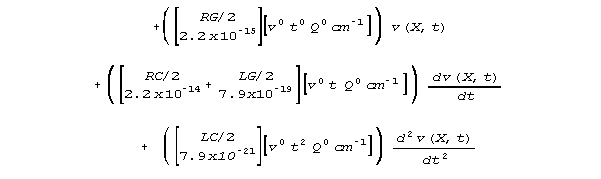
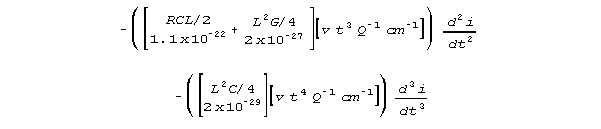
For this wire case, all the new crossterms are valid and finite terms, but they are numerically insignificant, far too small numerically to consider for modelling. The equation derived by the old limiting argument is operationally right (but not mathematically perfect). In the same notation as (8-wire) above, the reasonable equation to use is:

or, in simpler notation

or, yet more compactly

However, the picture is starkly different when one looks at equation 8 with numerical dimensional parameter values that correspond to a 1 micron diameter neural dendrite. Assuming reasonable values of axolemma conductivity, capacitance per membrane area, and inductance per unit length (volume conductivity 110 ohm-cm g = 3.18 x 10^-5 mho/cm² c=10^-6 farads/cm²) these numerical values are as follows:

R = 1.4 x 10¹⁰ ohm/cm L = 5 x 10^-9 henries/cm

C = 3.14 x 10^-10 farads/cm G = 3.14 x 10^-8 mho/cm

Note that R is 10¹¹ larger than in the previous case of the wire. The terms in equation 8 now have very different numerical values. Although most of the crossterms remain too small to consider, two crossterms are now dominant terms, and one of the primary terms, inductance, L, is too small to sensibly include in a modelling equation. In this regime, L is vastly smaller than the R²C/4 crossterm. Here is equation 8, with neural numerical values:

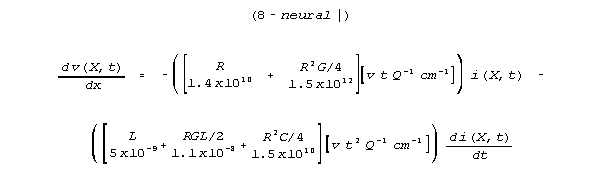
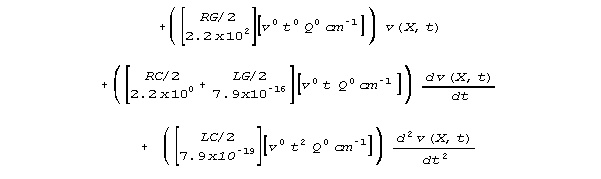
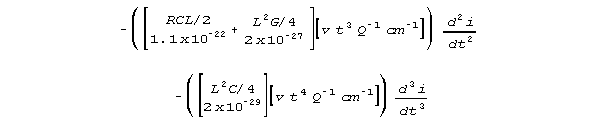
For this neural line case, the equation derived by the old limiting

argument is terribly misleading. The reasonable modelling

equation to use is

rather than

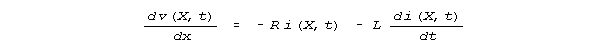
This paper has shown a new technique for deriving differential equations that is different from the usual one. It has put the new technique and the standard technique into the context of J.C. Maxwell's thought. It has illustrated the new technique, and argued for it, but has not proved it. A companion paper works though in more formal detail why it is necessary to use the notions of "length at a point", "area at a point", "volume a point", and "a point in time" rather than the incremental notions now used⁽²⁸⁾. Another companion paper illustrates the invalidity of our limiting arguments by example⁽²⁹⁾. A third companion paper illustrates, by a numerical example, that new terms derived according to Maxwell's first method can be (and very often are) far too small to matter quantitatively, but that under some other circumstances, these new terms can be dominant terms. In the case of neural transmission, consideration of the new terms predicts effective inductances 10,000,000,000 and more times the effective inductances predicted by Maxwell's second (and standard) method⁽³⁰⁾.

1. Department of Curriculum and Instruction, School of Education, University of Wisconsin, Madison, U.S.A. (email: showalte@macc.wisc.edu)

2. Department of Mechanical Engineering, Stanford University, Stanford Ca. USA

3. Kline, S.J. (1995) Conceptual Foundations for Multidisciplinary Thinking Stanford, Ca. Appendix C, p. 313.

4. Showalter, M.R. A (1997) Hypothesis: dendrites, dendritic spines, and stereocilia have resonant modes under S-K theory.

5. See http://www.santafe.edu/~johnson and Science Forums for THE NEW YORK TIMES at http://www.nytimes.com/.

6. Johnson, G. (1997) Proteins Outthink Computers in Giving Shape to Life NEW SCIENTIST March 25, 1997.

7. Showalter, M.R. Fully Hydrodynamic Piston and Cylinder Assembly U.S. Patent # 4,470,388, Sept 11, 1984.

8. Showaler, M.R., and Kline, S.J. A (1997) COUPLED PHYSICAL FINITE MODELS INVOLVE DIMENSIONAL PARAMETERS AND MUST BE SIMPLIFIED IN INTENSIVE FORM

9. Showalter, M.R., and Kline, S.J. B (1997) CONVENTIONAL LIMITING ARGUMENTS APPLIED TO PHYSICAL DIMENSIONAL MODELS SOMETIMES MISINTERPRET TERMS

10. Showalter, M.R. and Kline, S.J. C (1997) Equations derived by Maxwell's first method restrict the range of applicability of inferences from experiments.

11. Maxwell, J.C. (1878) DIMENSIONS Encyclopedia Britannica, 9th ed.

12. Showalter & Kline A pp. 11-15.

13. Showalter, M.R. B (1997) Reasons to doubt the current neural conduction model.

14. Regan, D. (1989) Human Brain Electrophysiology (Elsevior, New York) pp. 103-110.

15. Mathematicians may prefer to say that the equation at differentially small scale is as close to a differential equation as it can be in a measurable physical domain, and that this "differential equation" can be mapped into the domain of the algebra on a symbol-for-symbol basis.

16. Kline, S.J. (1965, 1984) SIMILITUDE AND APPROXIMATION THEORY McGraw Hill, New York; Springer-Verlag, ?????.

17. Showalter & Kline A pp. 12-14.

18. Showalter B.

19. Boyer, C. B. (1949, 1959) The history of the calculus and its conceptual development. (The concepts of the calculus) with a foreword by Richard Courant. -- Dover, New York.

20. Webster's Third New International Dictionary, unabridged, P.B.Gove, ed, Merriam-Webster, Springfield, Mass.

21. The International Dictionary of Applied Mathematics Van Nostrand, Princeton N.J. 1960.

22. Showater & Kline A p.8.

23. Showalter & Kline A pp. 12-14.

24. Showalter & Kline B pp. 5-12.

25. Showalter & Kline B.

26. Showalter & Kline A p. 22.

27. Showalter and Kline A pp. 12-14.

28. Showalter & Kline A.

29. Showalter & Kline A.

30. Showalter & Kline A pp. 2-5.