A verbatim copy of

by Christof Koch

taken from NATURE, 16 January, 1997

annotated and with two appendicesa1   a2

by   M.Robert Showalter

Evidence and argument are presented here supporting the position that current neuroscience data cited by Koch and connected to Koch's article, combined with the zoom FFT EEG measurements of David Regan, strongly supports the Showalter-Kline (S-K) passive conduction theory⁽¹⁾. The S-K theory appears to permit memory, and to imply processing speeds and logical capacities that are much more brain-like than permitted by the current Kelvin-Rall conduction model. The annotation of Professor Koch's article here is believed to be a good way to show how S-K theory fits in with what is now known and thought about neural computation. I argue that Regan's data, combined with the data cited and interpreted by Koch, requires the sort of sharp resonance-like brain behavior that occurs under S-K, that cannot occur under Kelvin-Rall.

Neurons and their networks underlie our perceptions, actions, and memories. The latest work on information processing and storage at the single-cell level reveals previously unimagined complexity and dynamism.

Over the past few decades, neural networks have provided the dominant framework for understanding how the brain implements the computations necessary for its survival. At the heart of these networks are simplified and static models of nerve cells. But neuroscience is undergoing a revolution^a0, and one consequence is that the picture of how neurons go about their business has altered.

a0. This annotation of Koch's article presents a new idea adapted to that revolution. The idea is that the current passive neural transmission equation (Kelvin-Rall) should be replaced with a new equation (Showalter-Kline, or S-K) that includes cross effects that yield two conduction modes, one much like that of Kelvin-Rall, the other a lower dissipation mode, where neural line conduction resembles electrical conduction in engineering conductors at much higher frequencies (at frequencies 10⁸ and more times the neural frequencies). Many of the "revolutionary" results in neuroscience are consistent under S-K (Appendix 2). Under S-K, neurons and groups of neurons are much more adapted for information processing than the same neurons would be under Kelvin-Rall.

To appreciate that, we need to start with a simple account of neuronal information processing. A typical neuron in the cerebral cortex, the proverbial gray matter, receives input from a few thousand neurons and, in turn, passes on messages to a few thousand other neurons (Fig. 1). These connections are hard wired in the sense that each connection is made by a dedicated wire^a1, the axon, so that, unlike processors in a computer network, there is no competition for communication bandwidth.

a1) Under S-K, both input and output of the neurons may occur by inductive coupling as well as direct conduction. When dendritic sections or spines are in the high transmission mode of S-K, neurons not directly connected can "communicate" by this inductive coupling.

Apart from the axons, there are three principal components of a neuron. The cell body (or soma); dendrites, which are short, branched extensions from the cell body, and which in the traditional view simply receive stimuli from other neurons and pass them on to the cell body without much further processing; and synapses, the specialized connections between two neurons.

Synapses are of two types, excitatory and inhibitory^a2. An excitatory synapse will slightly depolarize the electrical potential across its target cell, while an inhibitory input will hyperpolarize the cell. If the membrane potential at the cell body exceeds a certain threshold value, the neuron generates a millisecond-long pulse, called and action potential or spike. (Fig.2, overleaf). Otherwise, it remains silent. The amount of synaptic input determines how fast the cell generates spikes; these spikes are in turn conveyed to the next target cells through the output axon. Information processing in the average human cortex would rely on the proper interconnections of about 4 x 10¹⁰ such neurons in a network of stupendous size^b2.

a2) Under S-K, both excitatory and inhibitory synapses can also produce local changes in G that generate impedance mismatch reflections (and logical switching, including the trimming of resonant dendritic structures.) Changes in membrane resistance due to the opening state of populations of channels along a line can switch conduction properties from high dissipation properties essentially like those of Kelvin-Rall, to very low dissipation properties adapted to resonance.



b2) Under S-K, information processing in cortex relies on BOTH direct interconnections and the inductive coupling of switched, tunable, adaptive resonant structures.

In 1943, McCullough and Pitts showed that this (direct connection) view is at least plausible. They made a series of simplifications that have been with us ever since. Mathematically, each synapse is modelled by a single scalar weight, ranging from positive to negative depending on whether the synapse is excitatory or inhibitory. As a whole, the neuron is represented as a linear threshold element; that is, the contributions of all the synapses, multiplied by their synaptic weights, add linearly at the cell body. If the threshold is exceeded, the neuron generates a spike. McCollough and Pitts argued that, with the addition of memory, a sufficiently large number of these logical "neurons," wired together, can compute anything that can be computed on any digital computer^a3.

a3) McCullough and Pitts argued that "everything could be calculated" according to their suggested pattern. They did not show it. Major difficulties with the M & P case, in addition to the programming problem Koch treats below, concern speed, dissipation of information in neural lines (particularly when phase distortion is considered), and huge semirandom differences in transfer time due to the variable length of the connecting lines, that would be expected to smear out most or all of the fast logics that could be proposed. To an engineer who traces logic step-by-step, these all appear to be crushing difficulties. A difficulty that has gotten more attention than the others is the combinatorial explosion. If N is "sufficiently large" then N! is prodigious, a problem that has remained intractable in machine modelling from the start. For instance



(65! = 8.24x10⁹⁰ 66!=5.44x10⁹² 67!=3.64x10⁹⁴)



Under S-K there is inductive coupling of resonant "brain wave" signals that may contact or coordinate large numbers of neurons in broadcast mode, in addition to conductive coupling. Information content in resonant mode is huge, because the resonant properties predicted for known anatomy and physiology are very selective. The analogy to radar sending and receiving appears to be close. Resonant bandwidth of spines in the on state should typically be less than .001 Hz, with magnification factors, Q's, of 10⁴ and higher. The combination of on-state spines, dendritic sections, and synapses seems to be inherently arranged in a manner adapted to send (or receive) frequency-time signatures. Such signatures sent (in the proper phase relation with other oscillations) by means of an A.P. excitation will only be received in resonance by near-exactly tuned spine-dendritic section-synapse structures. "Brain wave" oscillation have long been observed. Because of inductive resonant coupling, line dissipation and transfer time dissipation constraints become much less important under S-K than in conduction path constrained models.



Under S-K, resonant interactions can occur contacting many (millions) of (reactive and nonreactive) neurons simultaneously. An analogy is the set of logical interactions that can occur among a population of people, all able to both broadcast and receive radio signals, where some may be tuned to the same wavelength and some not. The number of interactive combinations in such an interacting set is prodigious, and the coordinations possible very detailed. Under S-K, the neural network looks adapted for sending and receiving signals in the frequency domain. Frequency selectivity of dendritic spines and spine assemblies is inherently high (with predicted bandwidths often less than .001 Hz and predicted Q's above 1000). For such a system, a prodigious amount of information flow can occur by inductive means, with little or no crosstalk between many frequency-defined "bands". Under these conditions, the combinatorial limitation of neural nets that require connection essentially disappears.


Because resonant communication and processing is inherently a massively parallel process, it avoids the limitations of Feldman's "100 step rule."



Resonant processing is well adapted to "list reading" problems such as the lexical access problem, and can handle these in massive parallel, rather than sequentially. A major reason for rejecting "symbol processing AI" has been the inherent slowness and "anatomical implausibility" of the list-reading steps that AI algorithms so often contain. That constraint is removed by resonant access and processing, which appears to fit anatomy, and which is very fast.

Significant as their (McCollough and Pitts) result was, it left some major questions unanswered. Most importantly, how is such a network set up in the absence of an external programmer? A network of these abstract neurons has to be programmed from the outside to do any particular job, but the brain assembles by itself. Clearly, the information needed to provide a unique specification of the 2 x 10¹⁴ synapses in human cerebral cortex cannot possibly be encoded in the genome. Moreover, a key feature of biological nervous systems that radically distinguishes them from present-day computers is their ability to learn from previous experience, presumably by adjusting synaptic weights^a4. Finally the properties of real neurons are much more elaborate^b4 and variable (Fig 2b) than the simple and reliable units at the heart of McCullough and Pitts's neural networks and that of their progeny.

a4. the presumption that memory consists of synaptic weights and visible connections, and no more, was largely made in default of other physically testable, sensible alternatives. Under S-K, with its switched, bimodal transmission, both spines and dendritic sections have properties adapted to memory when combined with known channels and synaptic structures, including especially resonance. Under S-K, the information manipulating power of synapses and channels is MUCH MORE than under current theory. (For example, a single channel can switch a spine from "on" to "off" - (from a Q>10,000 state to a Q<10 state. When transmission under S-K is in the high dissipation mode, S-K and current theory produce almost the same results.



b4. Spines are an important example of that elaboration. Under S-K, dendritic spines, if in an all-channel closed state, appear to be very high Q resonant elements that may have LRC and column resonance modes that both have Q's of 10,000 or more, with resonant frequencies sensitive to geometry. With channel opening, these spines go to an "off" state of negligible resonance. Spines appear to be excellent memory components in the frequency domain, particularly in interaction with synapse switched dendritic sections with specific properties (that may be connected to other spines.) Means to change spine geometry as a function of resonant history can be learning means.

A possible mechanism addressing the need for self-programming was postulated a few years later by Donald Hebb: "When an axon on cell A is near enough to excite cell B and repeatedly or consistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased." Here, according to the principle known as synaptic plasticity, the synapse between neuron A and neuron B increases its "weight" if activity in A occurs at the same time as activity in B^a5

a5. Here is an analogous "neoHebbian" statement that may apply to on state spines and dendritic sections in the frequency domain.



"When a spine-dendrite assembly on cell A sends a frequency that is near enough to the resonant frequency of a spine-dendrite assembly on cell B so that the cell B spine is excited, and this resonant coupling occurs many times, some chemically mediated shaping process may occur to change the resonant frequency of the spine on Cell B so that it becomes MORE sensitive to the Cell A frequency signal."



This learning can be a selective process because spine resonant bandwidth may be less than .001 Hz.

Much of the excitement in the neural network revolution of the 1980's was triggered by the discovery of learning rules for determining the synaptic weights using variants of Hebb's rule of synaptic plasticity. These rules allow the synaptic weights to be adjusted so that the network computes some sensible function of its input - it learns to recognize a face, to encode eye position or to predict the stock market, for example.

Underlying these developments was the view that memory was stored in the synaptic weights. Changing connection strength can make the network converge to a different stable equilibrium, equivalent to recalling a different memory (associative memory, ref 3). Experimentally, the best studied aspect of increasing connection strength is long-term potentiation, which can be categorized as an increase in synaptic weight lasting for days or even weeks. It is induced by simultaneous activity in the pre-and postsynaptic terminals (Fig.1), in agreement with Hebb's rule. Of more recent vintage is the discovery of a complementary process, a decrease in synaptic weight termed long-term depression^a6.

a6. Both LTP and LDP become MORE IMPORTANT and more powerful information storage processes under S-K, because they can modulate frequencies, and because they can change firing thresholds of resonant structures.

These neural-network models assumed that, to cope with the apparent lack of reliability of single cells, the brain makes use of a "firing rate" code. Here, only the average number of spikes within some suitable time window, say a fraction of a second, matters. The detailed pattern of spikes was thought to be largely irrelevant (Fig, 2b). This hypothesis was supported by experiments in which monkeys were given the task of discriminating a pattern of moving dots amid background noise. The monkey's performance could be statistically predicted by counting spikes in single neurons within visual cortex, implying that all of the information needed to perform the task is available from the average firing rate alone. Further precision could in principle be obtained by averaging the firing rates over a large number of neurons (a process known as population coding), without any need to invoke the precise timing of individual spikes as a source of information^a7.

a7. Under S-K, many neural components (particularly spines, and lengths of dendrites switched between pairs of synapses) are inherently high precision components in resonant mode. That is useful from an "engineering" perspective. Averaging is a poor substitute for component precision in engineering practice for good reasons. Averaging takes time and space, and generally requires very high accuracy components within the averager apparatus. Typically, even if time is not at a premium, averaging approaches take many more precision components than accurate transduction means would have taken in the first place.

A snapshot of the "standard view" of information processing in the brain, say as of 1984, would be based on simple, linear-threshold neurons using firing-rate code that waxes and wanes over hundreds of milliseconds to communicate information among neurons. Memory and computation are assumed to be expressed by the firing activity of large populations of neurons whose synaptic weights are appropriately set by synaptic learning algorithms. But since then neuroscience has undergone a phase of exponential growth, with progress in three separate areas - in the study of dendrites, of spikes and their timing, and of synaptic plasticity.

ACTIVE DENDRITES

It was Ramon y Cajal who, in the late nineteenth century, first revealed the intricacies and complexities of real neurons. He showed that a prototypical neuron, say a cortical pyramidal cell as shown in Figs 1 and 3, has an extended dendritic tree which is scores of times larger in surface area than the cell body. It has become clear that dendrites do much more than simply convey synaptic inputs to the cell body for linear summation. Indeed, if this is all they did, it is not obvious why dendrites would be needed at all; neurons could be spherical in shape and large enough to accommodate all the synaptic inputs directly onto their cell bodies. A few neurons do follow this geometrical arrangement but the vast majority are more like the cell shown in Fig. 3, with an extended dendritic tree. This is where many of the synaptic inputs to the cell are received, but much of the membrane area is still devoid of synapses; so the function of the elaborate structure cannot simply be to maximize the surface area for synaptic contact.

Dendrites have traditionally been treated as passive cables, surrounded by a membrane which can be modelled by a conductance in parallel with a capacitor. When synaptic input is applied, such an arrangement acts as a low-pass filter, removing the high frequencies but performing no other significant information processing^a8. Dendrites with such passive membranes would not really perturb our view of neurons as linear threshold units^b8.

a8. Under S-K, the differential equation of conduction (in channel-closed, or low G mode) is of the same form as the standard electrical transmission equation. Transmission line effects seen in the gigahertz and higher range (including resonance and very sharp impedance mismatch switching) are reproduced in the neurological frequency range. Under S-K the dendrites that "appeared to the neuroanatomist Ramon y Cajal to be elaborate receiving antennae, studded with thousands of synapses⁽²⁾" are just that and more.



The dendrites are not "just antennae" - they are active components. Under S-K, the dendrites contain a great deal of spatially detailed switching capacity, with each synapse capable of impedance mismatch switching, with channels in the aggregate switching transmission from a very high dissipation to a very low dissipation conduction mode, and with the spines as very high Q coupled, switched resonators at many places on the dendrite. This dendrite is a receiver, a sender, and a processor of information by inductive means, and also transmits by conduction in the long-studied ways.



b8. Under S-K, dendrites are much more complicated than linear threshold units even if they are passive (in the sense of acting without any openings or closings of channels or synapses) because of resonant effects. When synaptic and channel activity is added, the complication (and information handling and learning capacity) greatly increases.

But dendrite membranes are not passive - they contain voltage-dependent membrane conductances. These conductances are mediated by protein complexes that allow charged ions to flow across the membrane. As long ago as the 1950's, Hodgkin and Huxley showed how the transient charges in such conductances generate and shape the action potential^a9. But it was assumed that they are limited to the axon and the adjacent cell body. We now know that many dendrites of pyramidal cells are endowed with a relatively homogeneous distribution of sodium conductances as well as a diversity of calcium membrane conductances^b9.

a9. Hodgkin and Huxley were very clear about whole-axon action potentials. They were not so clear about how their action potential propagated down a neural line. The Kelvin equation is a standard electrical engineering equation (with L negligible) and the behavior of the (Kelvin-Rall) RC line shows conduction velocity that varies as the square root of (fourier component) frequency⁽³⁾. Whether that RC line is propagating passively or in a channel amplified mode, the observed coherence of A.P. waveform (which has many very different fourier components) during propagation seems impossible. The high frequency components should outrun the low frequency components, and they do not. With S-K, that difficulty is removed, because different fourier components propagate at the same velocity. Calculated and observed A.P. propagation velocities seem to match predictions under S-K. The logic of the action potential that Hodgkin and Huxley set out in most detail fits S-K well, but is incompatible with the Kelvin-Rall model now used.



b9. Even if difficulties due to differential velocity of different fourier components under Kelvin-Rall is set aside, there is another major difficulty. Any heterogeneity of channel conductances offers difficulty for A.P. propagation under Kelvin-Rall, because that model depends on a continuous and differentiable amplification to compensate for the inherently very dissipative passive mode of propagation under Kelvin-Rall. Very uniform channel densities are also needed to avoid impedance reflection effects. Observations seldom seem to show totally smooth channel densities along dendrites. There is more reason to believe heterogeneity is the rule - indeed Zecevic⁽⁴⁾ showed stunning heterogeneity, with "multiple spike initiation zones" in an axon that showed rather conventional A.P. behavior. These results are inconsistent with Kelvin-Rall, but are consistent with S-K, which has a high effective line inductance and far less dissipation than predicted under Kelvin-Rall.

What is the function of these active conductances? In a passive cable structure, synaptic input to the more distant regions of the dendritic tree (as the to of Fig.3) would quickly saturate, delivering only a paltry amount of electric current to the spike initiating zone far away^a10. But it turns out that synaptic input to this part of the tree is sufficient to elicit somatic action potentials, and the likely explanation (supported by computer models) is that calcium and potassium membrane conductances in the distant dendrites can selectively amplify this input^b10.

a10. Under S-K, dissipation will be much less than in Kelvin-Rall, but still important enough to provide good reason for amplification.



b10. Under S-K, calcium and potassium conductances can still amplify as argued in Bernander, Koch, and Douglas. However, there is somewhat less need for amplification, and the conductances can be logically active in other ways.

Voltage-dependent conductances can also subserve a specific nonlinear operation, multiplication. In a passive dendritic tree, the effect of two synaptic inputs is usually less than the sum of the two individual inputs; that is, they show saturation. This saturation effect can be minimized by spreading the synapses far apart. If, however, the dendritic tree contains sodium and calcium conductances, or if the synapses use a particular kind of receptor (the so-called NMDA receptor), the inputs can interact synergistically: now, the strongest response occurs if inputs from different neurons are located close to each other on a patch of dendritic membrane. Computer simulations show that such a neuron effectively performs a multiplication; that is, its firing rate is proportional to the product, rather than the sum, of its inputs. Multiplication is one of the most common operations carried out in the nervous system (for example, for estimating motion or the time-to-contact with an approaching stimulus), and it is tempting to speculate that this may be achieved through such processes at the cellular level.

A further development has been the realization that the distribution of calcium ions within dendrites may represent another crucial variable for processing and storing information. Calcium enters the dendrites through the voltage-gated channels, and this, along with its diffusion, buffering and release from intracellular stores, leads to rapid local modulations of calcium concentration within the dendritic tree. The concentration of calcium can, in turn, influence the membrane potential (through calcium-dependent membrane conductances) and - by binding to buffers and enzymes - turn local biochemical signalling pathways on or off^a11.

a11. Under S-K, calcium can switch propagation between a low dissipation mode and a (Kelvin-Rall like) high dissipation mode by changing g.

It was also Ramon y Cajal who postulated the law of "dynamic polarization,' which stipulates that dendrites and cell bodies are the receptive areas for the synaptic input, and that the resulting output pulses are distributed unidirectionally along the axon to its targets. This assumes that action potentials travel only along axons: no signal was thought to travel outwards along the dendrites.

From work on brain slices, however, it seems that this is by no means the whole story. Single action potentials can propagate not only forwards from their initiation site along the axon, but also backwards into the dendritic tree (a phenomenon known as "antidromic spike invasion"). It remains unclear whether dendrites can initiate action potentials themselves. If they can, such dendritic spikes could support theoretical proposals that all-or-none logical operations occur in the dendritic tree. The next step will be to find out whether action potentials can propagate into the dendritic tree under more natural conditions - that is, using sensory stimuli in an intact animal.

Thus, it is now evident that the dendritic tree is far more complex than the linear cable models of yesteryear assumed. Dendrites provide the substrate for numerous nonlinear operations, and endow neurons with much greater information-processing capacity than was previously suspected^a12.

a12. Change to S-K, and complexity increases, precision increases, and information processing ability increases. Resonance-mediated memory, including spine resonance and synapse switched dendritic section resonance, becomes available. The dendrites become able to send and receive frequency coded information over long distances via inductive coupling. The logical importance of individual synapses and groups of channels is much greater under S-K than under Kelvin-Rall.

TIMING COUNTS

The second area in which our thinking has changed has to do with the role of time in neuronal processing. There are two main aspects to this issue - first, the relationship between the timing of an event in the external world and the timing of the representation of that event at the single-neuron level; second, the accuracy and importance of the relative timing of spikes between two or more neurons.

Regarding the first question, some animals can discriminate intervals of the order of a microsecond (for instance, to localize sounds), implying that the timing of sensory stimuli must be represented with similar precision in the brain^a13. But this usually involves highly specialized pathways, probably based on the average timing of spikes in a population of cells^b13. However, it is also possible to measure the precision with which individual cells track the timing of external events. For instance, certain cells in the monkey visual cortex are preferentially stimulated by moving stimuli, and these cells can modulate their firing rate with a precision of less than 10 ms (ref 16).

a13. Under S-K, wave propagation (and reflection) in dendritic spines and dendritic sections is precise enough that single components can be very accurate timers, particularly for resonant columns detecting and comparing spike-containing signals. For example stereocilia are 1/4 wave resonant columns, constructable from 10 Hz to 150,000 Hz, with geometries consistent with known stereocilia anatomy. With S-K, the "engineering difficulty" of building a microsecond sensitive timer and interval representation component is large, but it is a much easier job than would be involved with Kelvin-Rall.



b13. With S-K, averaging may not be necessary. Single component accuracy should be good enough. (If it isn't, how does averaging help you? You must, after all make your averaging apparatus out of something real. Averaging soaks up time and space. The total system has to be very good indeed if you have to process as much information as a bat does.)

The second aspect of the timing issue is the extent to which the exact temporal arrangement of spikes - both within a single neuron and across several neurons - matters from information processing. In the past few years there has been a resurgence of signal processing and information-theoretical approaches to the nervous system. In consequence, we now know that individual neurons, such as motion-selective cells in the fly or single auditory inputs in the bullfrog, can encode between 1 and 3 bits of sensory information per strike, amounting to rates of up to 300 bits per second. This information seems to be encoded using changes in the instantaneous interspike interval between a handful of spikes^a14. Such a temporal encoding mechanism is within 10-40 per cent of the theoretical maximum allowed by the spike train variability. This is quite remarkable because it implies that individual spikes in a single cell in the periphery can carry significant amounts of information, quite at odds with the idea that neurons are very unreliable and can only signal in the aggregate. At these rates, the optic nerve, which contains about one million fibers, would convey between on and a hundred million bits per second - compare this with a quad-speed CD-ROM drive, which transfers information at 4.8 million bits per second.

a14. Under S-K, spines and dendritic sections are well adapted to compare interspike intervals, particularly in high Q column resonant mode (long spines).

The relative timing of spikes in two or more neurons can also be remarkably precise. For instance, spikes in neighboring cells in the lateral geniculate nucleus, which lies midway between the retina and the visual cortex, are synchronized to within a millisecond. And within the cortex, pairs of cells may fire action potentials at predictable intervals that can be as long as 200 ms, two orders of magnitude longer than the delay due to a direct synaptic connection, with a precision of about 1 ms^a15. Such timing precision across populations of simultaneously firing neurons is believed to be a key element in neuronal strategies for encoding perceptual information in the sensory pathways^b15.

a15. Under S-K, with inductive coupling via the extracellular medium, this coordination is exactly what one would expect.



b15. To keep a frequency domain code straight, oscillatory coordination is extremely desirable so that frequency-temporal messages can be sent and received at standard cycle times. (Radar technology has many examples of this sort of signal timing, and so does ordinary language.)

If neurons care so much about the precise timing of spikes - this is, if information is indeed embodied in a temporal code - how, if at all, is it decoded by the target neurons? Do neurons act as coincidence detectors, able to detect the arrival time of incoming spikes at millisecond or better resolution? Or do they integrate more than a hundred or so relatively small inputs over many tens of milliseconds until the threshold for spike initiation is reached? (Ref 23, Fig 2a) These questions continue to be widely and hotly debated^a16.

a16. Under S-K, dendrite-spine assemblies are well adapted to receive temporal code via resonant inductive coupling. Decoding by resonance is inherent when tuning occurs. A significantly strong signal can fire action potentials. Signal resolution can be considerably better than 1 millisecond. Averaging is not necessary.

SYNAPTIC PLASTICITY

Back-propagating action potentials are puzzling if considered solely within the context of information processing^a17. But they make a lot of sense is seen as "acknowledgement signals" for synaptic plasticity and learning. A Hebbian synapse is strengthened when pre and postsynaptic activity coincide. This can occur if the presynaptic spike coincides with the postsynaptic spike that is generated close to the cell body and spreads back along the dendritic tree to the synapse. A new and beautiful study shows that the order of the arrival time between the presynaptic spike and the back-propagated postsynaptic spike is critical for synaptic plasticity.

a17. In a system with switched resonance, backpropagating a.p.'s make sense for processing, as well as for learning.

If the presynaptic spike precedes the postsynaptic spike, as should occur if the first participates in triggering the second, then long term potentiation occurs - that is, the synaptic weight increases. If, however, the order is reversed, the synaptic weight decreases. So sensitive is this sequence that a change of timing of as little as 10 ms either way can determine whether a synapse is potentiated or depressed^a18. The purpose of this precision is presumably to enable the system to assign credit to those synapses that were actually responsible for generating the postsynaptic spike.

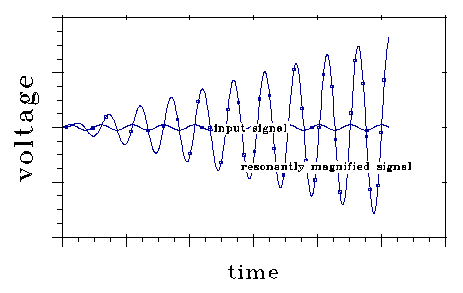
a18. In resonance, which is to be expected under S-K, the notion that a phase difference may either magnify or reduce a response (or, by a small extension, a weight) comes naturally. Here is a curve showing resonant magnification, with the perturbation (input) signal phased so that resonance builds up. It, at some time t, input signal phase shifted 180 degrees, the resonant signal would decrease at the same rate. Around null, a shift of a few degrees makes the difference between rather rapid resonant signal increase and rapid decrease. FM radio operates on this principle. This property of a resonant system can be used to increase its ability to carry and process information.

These (time sensitive) experiments come at a fortuitous time, for theoretical work has begun to incorporate asymmetric timing rules into neural network models. The attraction of doing so is that it allows the network to form associations over time, enabling it to learn sequences and predict events. It is therefore gratifying to find that synapses with the required properties do indeed exist within the brain.

In the past year there has also been the emergence of a new way of thinking about short-term plasticity, one that complements the view of long-term synaptic changes for memory storage. This has come about by joint experimental-theoretical work (refs 26, 27, see overleaf), suggesting that individual synapses rapidly adapt to the presynaptic firing rate, primarily signalling an increase or a decrease in their input. That is, synapses continuously adapt to their input, only signalling relative changes, which means that the system can respond in a highly sensitive manner to a constantly and widely varying external and internal environment^a19. This is entirely different from digital computers that enforce a strict segregation between memory (onboard cache, RAM, or disk) and computation. Indeed they are carefully designed to avoid adaptation and other usage dependent effects from occurring.

a19) Under S-K, this might better read "synapse-dendritic section assemblies continuously adapt to their input, so that they only signal relative changes, which means that the system can respond in a highly sensitive manner to a constantly and widely varying external and internal environment." The rephrasing would maintain the thrust of the logic, and would be consistent with observations.

Interestingly, single-transistor learning synapses - based on the floating gate concept underlying erasable programmable ROM digital memory - have now been built in a standard CMOS manufacturing process. Like biological synapses, they can change their effective weight in a continuous manner while they carry out computations. Floating-gate synapses will greatly aid attempts to replicate the functionality of nervous systems by the appropriate design of neuromorphic silicon neurons using analog very-large-scale-integrated (VLSI) circuit fabrication technology.

HYBRID COMPUTER

Overall, then, current thinking about computation in the nervous system has the brain as a hybrid computer. Individual nerve cells convert the incoming streams of digital pulses into spatially distributed variables, the postsynaptic membrane potential and calcium redistribution. This transformation involves highly dynamic synapses that adapt to their inputs^a20.

a20) Under S-K, "highly dynamic synapses" would be interpreted as "highly dynamic synapse-dendritic section assemblies."

Information is then processed in the analog domain, using a number of linear and nonlinear operations (multiplication, saturation, amplification, thresholding^a21) implemented in the dendritic cable structure and augmented by voltage dependent membrane and synaptic conductances. The resulting signal is then converted back into digital pulses and conveyed to the following neurons^b21. The functional resolution of these pulses is in the millisecond range, with temporal synchrony across neurons likely to contribute to coding. Reliability could be achieved by pooling the responses of a small number (20-200) of neurons^c21.

a21. Also resonance under S-K.



b21. Under S-K, conduction and inductive coupling through the intercellular medium both occur.



c21. Under S-K, reliability and precision in resonant or time delay mode is inherently high, and averaging is unnecessary or less necessary.

And what of memory? It is everywhere (but can't be randomly accessed). It resides in the concentration of free calcium in dendrites and the cell body; in the presynaptic terminal; in the density and exact voltage-dependency of the various ionic conductances; and the density and configuration of specific proteins in the postsynaptic terminals^a22.

a22. Under S-K, much more specific memory than that described above follows near-inherently from anatomy. The resonant memory structures are more adapted to learning and to rapid readout of memory from large volumes of cells, for jobs like lexical access. Spines are very high Q resonant objects (with both LRC and column resonance modes) that are channel switched on and off. Plausible modifications seem simply adapted to let spines "learn" different pitches through a mechanism like LTP. Spine-dendrite-synapse assembly states seem adaptable to store temporal signatures of high information content in resonance, and to respond to such coded stimuli in stereotyped ways (generating action potentials). With action potentials serving to excite resonant dendritic structures, temporal signatures may also be "broadcast" into the extracellular medium. This view fits the very sharply resonant data of David Regan (Appendix). Regan's fast FFT EEG measurements under evoked conditions routinely measured resonantly organized signals in sharp patterns with many peaks with bandwidths as tight as .002 Hz or tighter. Regan's data may be interpreted to show the combined effect of large populations of sharply resonant spines, and match model predictions under S-K.



It appears that all the learning modes suggested by Koch and others also continue to be available under S-K.

Only very little of this complexity is reflected in today's neural network literature. Indeed, we sorely require theoretical tools that deal with signal and information processing in cascades of such hybrid, analog-digital computational elements. We also need an experimental basis, coupled with novel unsupervised learning algorithms, to understand how the conductances of a neuron's cell body and dendritic membrane develop in time. Can some optimization principle be found to explain their spatial distribution?

As always, we are left with a feeling of awe for the amazing complexity found in nature. Loops within loops across many temporal and spatial scales. And one has the distinct feeling that we have not yet revealed every layer of the onion^a23. Computation can also be implemented biochemically - raising the fascinating possibility that the elaborate regulatory network of proteins, second massagers and other signalling molecules in the neuron carry out specific computations not only at the cellular but also at the molecular level.

a23. Under S-K the old data remains important, and much of the old theory does as well. (One of the modes of S-K is nearly identical to Kelvin Rall.) But the information processing capacity of individual dendrites and neural tissue becomes much greater under S-K, and the capacities of brain become somewhat more comprehensible.

ARTICLE INSERT: THE ADAPTABLE SYNAPSE^a24

In short-term synaptic depression, the postsynaptic response to a regular train of presynaptic spikes firing at a fixed frequency f gradually lessens. The response of the first spike might be large, but subsequent responses will be diminished until they reach a steady state (expressed in terms of A, the fractional reduction in postsynaptic effect). This is shown here (part a) for presynaptic spikes at 40 Hz frequency (data from ref 26).

This depression generally recovers within 0.1 to 0.5 s. For firing rates above 10 Hz, A is roughly inversely proportional to the firing frequency. In other words, within a few hundred milliseconds the synapse will have adapted to the presynaptic firing with a response roughly independent of the firing rate (due to the inverse relationship between A and f). If the synaptic

consequence, the transient change in the postsynaptic response will be proportional to the relative change in firing frequency. This is demonstrated in computer simulations in which the presynaptic firing rate of a couple of hundred such synapses converging onto a model neuron is increased fourfold (part b - the increases are from 25 to 100 Hz on the left and from 50 to 200 Hz on the right; data from ref. 27).

Even though the final input rate is twice as high on the right side as on the left, the firing rate of the neuron is roughly the same. This is because the fractional increase - relative to the background rate - is the same in both cases. This form of short-term depression in synaptic strength therefore enables synapses to respond to relative changes in firing rates rather than to absolute rates.

a24) Under S-K, none of the interpretations Koch discusses in this insert need change (one of the modes under S-K is nearly identical to Kelvin-Rall). However, under S-K adaptations may also be by means of dendritic section (or spine) synapse assemblies, rather than synapses alone. For such assemblies, the precise timing of wave propagation, and the sensitivity of S-K to local values of g could produce rapid, sensitive adaptation.

Appendix 1.   Resonance in neurons, as measured, and as calculated by S-K theory.

David Regan has measured brain magnetic fields (MEG) and scalp voltages (EEG) during evoked stimulation. Figs 9 and 10⁽⁵⁾ show some of Regan's measurements using his zoom FFT technique.

a1

Fig. 9

The caption for this figure reads:

"The stimulus was a homogeneous patch of light flickering at F₁ superimposed on a second patch flickering at F₂. The EEG was analyzed by nondestructive zoom FFT at resolution of 0.0039 Hz. Recording duration was 320 seconds. The section contains 12,000 lines over a bandwidth of .5 - 49.5 Hz. The steady-state evoked potential consists of discrete frequency components whose bandwidths are less than 0.0039 Hz. . . . " The data have characteristics often seen in resonant systems with very low damping, with sums and integer multiples of the stimulus."

Figure 10 shows evidence of bandwidths narrower than bin widths of .0019 Hz. The 4F component is shown. Bandwidths of the peaks measured in Fig 9 may have been no wider than this.

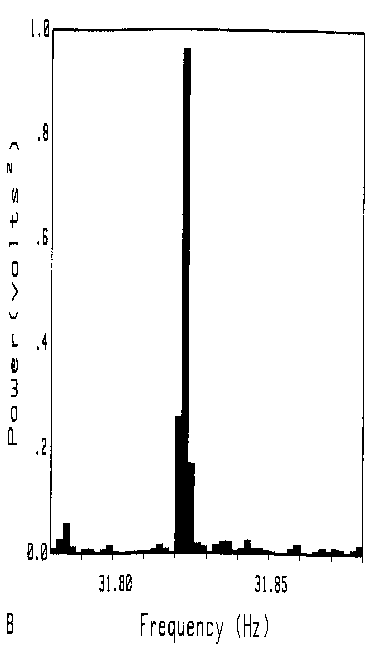
Fig. 10

These sharp, high information content patterns, with stimuli frequency multiples organized roughly as shown, show that brain includes sharply resonant components, and shows that these components are coupled with very small lags and with small damping. The bandwidths Regan measures are too sharp by at least an order of magnitude to be produced by membrane channel activity.

The pyramidal cells in brain, interpreted according to the S-K theory, should behave in a manner that generates the kind of behavior that Regan measured. Conduction lines have very low distortion. Effective line inductances are far greater than those predicted by Kelvin-Rall - high enough so that neurons can be inductively coupled via the intercellular medium, which conducts millions of time faster than line conduction speed. The dendritic spines have the sharply resonant requirements Regan's data appears to require.

Resonance:

Resonance is logically interesting. Enormous resonant magnifications of tightly selected signals are possible. In this sense, resonant systems can function as highly selective amplifiers. This fact is a foundation of communication technology. Radio and television offer familiar examples of resonant selectivity. Radio and television receivers exist in an electromagnetic field consisting of a bewildering and undescribable variety of electromagnetic fluctuations. Reception occurs because the resonant receiver is selective for a specific frequency at a high degree of phase coherence. Signals off frequency are not significantly detected, and "signals" of random phase that are on frequency cancel rather than magnify in resonance. Radar receivers also operate on the principle of resonance. Other examples are our telephone system and cable television system, each organized so that a multiplicity of different signals can be carried in physically mixed form over the same conduits. These "mixed" signals can be separated and detected with negligible crosstalk by resonant means.

Electrical resonance can store up energy in an oscillation having a peak voltage Q times the oscillating voltage of the exciting disturbance. Resonant systems may all be described in wave propagation terms, and many can also be treated in lumped terms. The LRC oscillator common in differential equation textbooks is an example of a resonant system described in lumped terms.

The International Dictionary of Applied Mathematics explains inductance-resistance-capacitance (LRC) series resonance as follows, and describes behavior generally characteristic of resonance. The "coil" is a lumped inductance, the "condenser" is a lumped capacitance, and "j" is the square root of -1.

. . . In an a-c circuit containing inductance and capacitance in series ... the impedance is given by

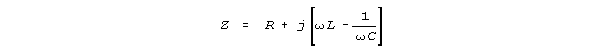
L is the inductance, and C is the capacitance. It can be readily seen that at some frequency the terms in the bracket will cancel each other, and the impedance will equal the resistance alone. This condition, which gives a minimum impedance (and thus a maximum current for a fixed impressed voltage) and unity power factor is known as series resonance. Where the resistance is (relatively) small the current may become quite large. As the voltage drop across the condenser or coil is the product of the current and the impedance of that particular unit, it may also become very large. The condition of resonance may even give rise to a voltage across one of these units that is many times the voltage across the whole circuit, being, in fact, Q times the applied voltage for the condenser and nearly that for the coil. This is possible since the drops across the coil and condenser are nearly 180 degrees out of phase, and thus almost cancel one another, leaving a relatively small total voltage across the circuit . . .⁽⁶⁾

Fig 11 shows how the voltage oscillation stored in a resonant system grows when it is driven by a input signal at its resonant frequency. The growth shown depends on stimulus phase, a fact on which FM transmission depends. If, at some time, the input signal voltage shown were to shift phase 180 degrees, the resonant voltage would decrease as fast as it is shown increasing here.

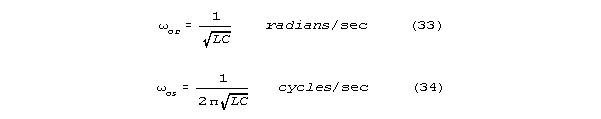
The resonant amplification factor, Q, achieved after time to equilibrium⁽⁷⁾, is:

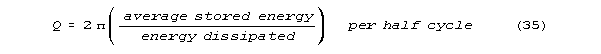
For an LRC resonator, Q is

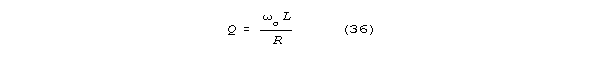
High Q's are prized in information processing systems, partly because bandwidth (the frequency difference between the half power points on a resonance curve) is inversely related to Q according to the formula:

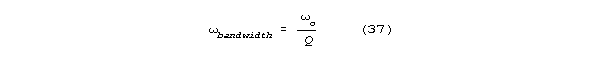
For spines, Q's in the tens of thousands are possible.

Columns can also be sharply resonant. Columns (transmission lines) of 1/4 and 1/2 wavelength have been used as resonators in musical instruments for many centuries. More recently, column resonance has been used with precision in the radar and communication fields. Well terminated lengths of neural passage that are sharply open (short circuited) at both ends are resonant when there length is exactly 1/4 of wavelength. For column length l_c:

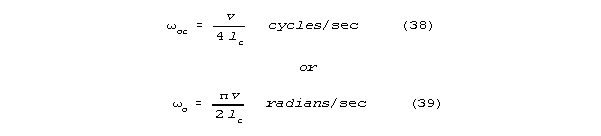
and integer multiples of resonant frequency, omega_o. A well terminated length of neural

passage that sharply closed on one end will be resonant at

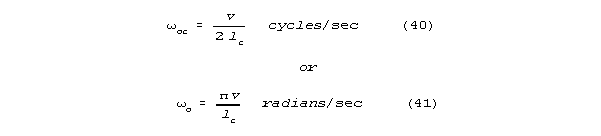
and integer multiples of these frequencies.

For a neural line in the constant velocity regime:

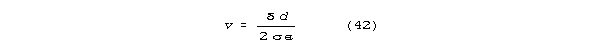
As a 1/4 wave resonant column of length l_c:

.

Q of the column resonator will be inverse with attenuation per

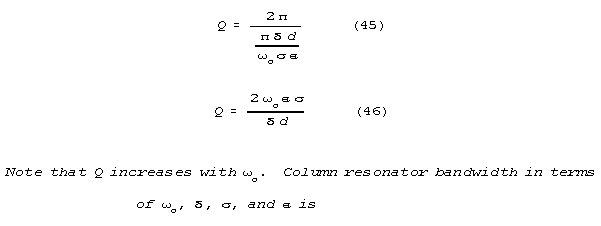
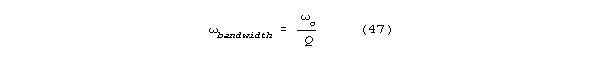
Column resonators are more powerful information handling devices than lumped resonators of the same Q, because they magnify and store repeating WAVEFORMS that fit as standing waves within them. (For this reason, a wind instrument or pipe organ wave form can be much more complicated than a sine wave.) In contrast, an LRC resonator stores a sine wave.

The brain appears to be a resonant system, and if it may be judged by the Q's it shows, a very capable one. Considering Regan's frequencies of 7-46 Hz, and setting _bw at .0019 Hz, we calculate Q's of 3680 to 24,200 for the ensembles that represent frequency peaks. These are very high calculated ensemble Q's, higher than the Q's of even the best nonsuperconducting tuned circuits. Individual resonator Q's must be higher still. Regan's measurements give upper bounds on bandwidths. From neuroanatomy, the candidate resonant structure seems plain - the dendritic spines. There are about 10¹³ dendritic spines in brain, and, based on the values of effective inductance predicted here, the spines appear to be resonant structures with very high resonant amplification factors (Q's).

SPINE ANATOMY AND SPINE RESONANCE:

Fig 12⁽⁸⁾ shows camera lucida drawings of a neuron body and proximal dendrites of a rat hippocampal (CA1) neuron showing common spine types: thin, mushroom shaped, and stubby. The "thin" type is the commonest in cortex (about 70%), and can be considered as both an LRC element and a column resonant element. In LRC mode, the bag and shaft have a lumped capacitance, and shaft inductance and resistance are considered in lumped form. In column mode, the shaft is a column open at both ends, with a termination correction.

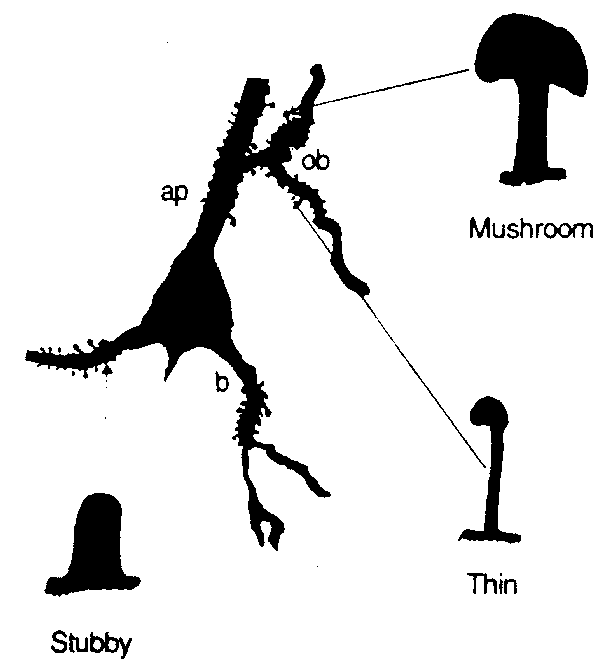
Figure 13 shows an electrical model of a thin spine. In the scaled figure, 4/5 of spine capacitance is in the bag section.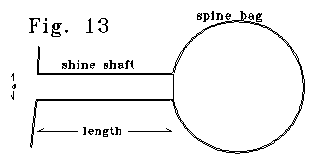

The "spine" of Fig. 13 can be modelled as an LRC resonant system. Capacitance is the capacitance of the "bag" section, plus half the capacitance of the shaft section. The shaft has resistance of R, and an effective inductance of L_edelta x. The L_e/R ratio is inverse with diameter. Different bag sizes for the same shaft size yield different LC products, and different resonant frequencies. Q, radian frequency, and bandwidth, for the LRC case are:

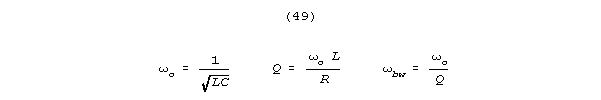
In the model, bandwidth is proportional to diameter. Let's arbitrarily chose a shaft diameter of .1 micron, shaft length of

.5 micron, interspine medium conductance of 110 ohm-cm, membrane capacitance of 1 microfarad/cm², and zero membrane leakage, g. Holding these values, and varying bag size, yields the following relation between frequency and Q.

Q = _o(910)

For Regan's measured frequency range of 7-45 hz (44-283 radians/sec,) Q's between 40,000 and 257,000 are estimated. Regan's data correspond to Q's about a decade smaller, between 3,680 and 24,000 over that same 7-45 Hz frequency range. This is an acceptable fit because:

Regan must have measured ensemble properties, not properties of single neural elements.

Regan's setup could have detected no tighter bandwidths than he did detect. and

Within the constraints of biological knowledge, we could have guessed other values of the parameters to come closer to Regan's values (or even to match them.)

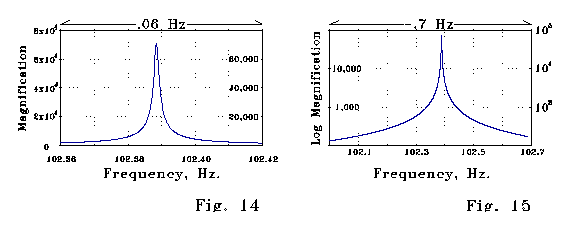
Figs 14 and 15 below show steady-state magnification of a signal as a function of frequency calculated for the LRC spine model of Fig 13. The peak magnification factor is about 70,000. Note the sharpness of the magnification as a function of frequency.

The model spine of Fig 13 would also have a column resonance mode. Spine column resonant frequency will be approximately

and could estimate column resonant Q from equation () as

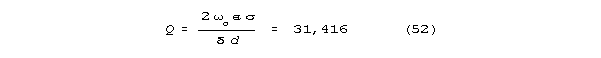
Electrical compliance of the bag would shift these resonant frequencies and Q's somewhat from the simple 1/4 wave column calculation set out above, but the correction would involve details that can be considered elsewhere.

Referring again to Regan's data, the brain has many (about 10¹³) spines. If spine resonant frequencies are widely distributed, and some reasonable fraction of the dendritic spines are in the high Q state, one would expect fixed frequency stimuli, such as Regan supplied, to yield the sort of excitation curves that Regan observed. Coupling of the spines would be via the very rapid conduction of the extracellular medium, not via conduction along dendrites or axons.

SPINE SWITCHING:

Spines are adapted for off switches. A single membrane channel can turn off spine resonance. This may be useful

because otherwise, voltage buildups sufficient to break down the dielectric of the spine bags, with consequent spine destruction, might occur⁽⁹⁾ and

because binary switching is useful in information processing.

Suppose there is one membrane channel in the bag portion of the spine. If that channel is open, it acts as a shunt, damping voltage fluctuations that occur across it. There will be a shunt across the bag membrane. The spine will have a shunt limited Q, Q_damped. Let R_c be shunt channel resistance. If Q_damped<<Q, as it will be for a channel, we can say that:

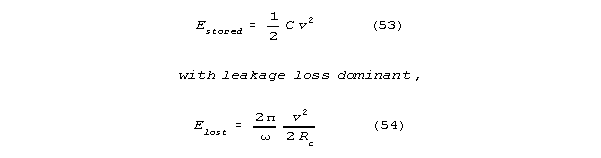
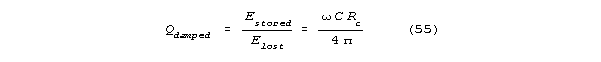
The Q_damped << Q assumption makes sense for reasonable membrane channel values (between 4 and 400 picosiemens⁽¹⁰⁾.) Opening of one channel will change a spine from a sharply resonant state, with a Q in the thousands, to a Q less than 10, a very wide bandwidth state. A single channel therefore acts as an on-off switch.

Evidence and argument has been presented here supporting the position that current neuroscience data cited by Koch and connected to Koch's article, combined with the zoom FFT EEG measurements of David Regan, strongly supports the Showalter-Kline (S-K) passive conduction theory. That theory appears to permit memory, processing speeds and logical capacities that are much more brain-like than permitted by the current Kelvin-Rall conduction model. The annotation of Professor Koch's article was employed here as a good way to show how S-K theory fits in with what is now known and thought about neural computation. Regan's data, combined with the data cited and interpreted by Koch, requires the sort of sharp resonance-like brain behavior that occurs under S-K, that cannot occur under Kelvin-Rall.




Appendix 2: The S-K transmission equations:

The currently accepted passive neural conduction equations are the standard conduction equations of electrical engineering, usually written in a contracted form that discards the terms in L that are negligible in this equation.

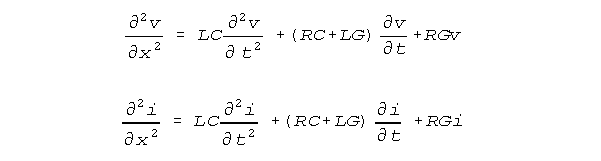
Robert Showalter and Stephen Jay Kline have found that these equations lack crossterms because special restrictions on the use of dimensional parameters in coupled finite increment equations have not been understood⁽¹¹⁾

. The crossterms, which can also be derived (within a scale constant) by standard linear algebra based circuit modelling, are negligible in most engineering applications. But these crossterms are very large in the neural context. The Showalter-Kline (S-K) equations are isomorphic to the standard conduction equations of electrical engineering and are written as follows.

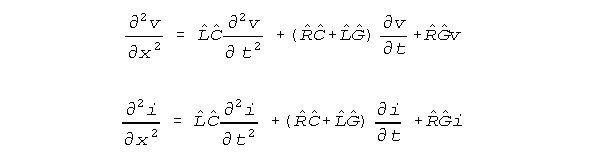
For set values of resistance R, inductance L, membrane conductance per length G, and capacitance C, these equations have the solutions long used in electrical engineering. The hatted values are based on a notation adapted to crossproduct terms. In this notation, the dimensional coefficients are divided into separate real number parts (that carry n subscripts) and dimensional unit groups, as follows.

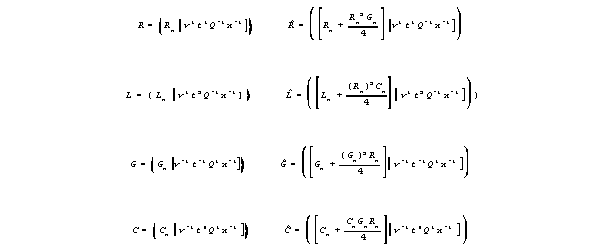
For wires,, the crossproduct terms are negligible, and the two kinds of equations are the same. But under neural conditions the crossproduct terms are LARGE. For instance, effective inductance is more than 10¹² times what we now assume it to be. The S-K equation predicts two modes of behavior.

When G is high (some channels are open) behavior similar to that of the current model is predicted.

When G is low, transmission has very low dissipation, and the system is adapted to inductive coupling effects including resonance.

Under S-K, attenuation of waves per wavelength or per unit distance varies over a much larger range than occurs in the now-accepted theory. There is a low membrane conductance regime where attenuation of waves is small, and wave effects are predicted. However, as channels open attenuation increases enormously, and waves may be damped out in a few microns. Under the new model a neural passage can be either sharply "on" or sharply "off" depending on the degree of channel-controlled membrane conductance. In the high g regime, attenuation per wavelength values are qualitatively similar for the Kelvin-Rall and S-K.

Figures 2, and 3 plot unit wave amplitude after one wavelength (right axis) or damping exponent per wavelength (left axis) as a function of membrane conductance, g, for both Kelvin-Rall and S-K theory. The curves map functions that move rapidly - exponents are graphed in log-log coordinates.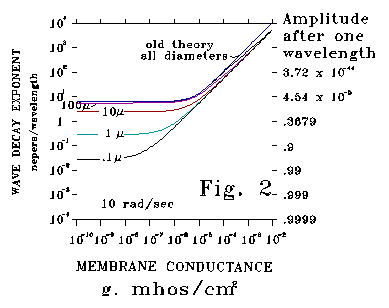

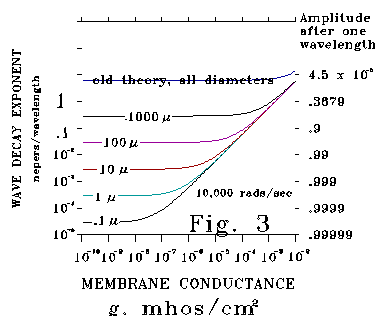
Figure 2 plots calculated responses at the low frequency of 10 radians/second for neural process diameters ranging over five decades (from 1000 microns to .1 micron). For the 1000 and 100 micron cases the Kelvin-Rall and S-K curves are almost the same. Results for these large diameters and low frequencies are also nearly the same on an attenuation per unit length and a phase distortion basis. These conditions correspond to squid axon experiments that are famous tests of the Kelvin-Rall theory. However, for smaller diameters, attenuation according to S-K theory is much less than that according to Kelvin-Rall.

Figure 3 plots calculated responses at 10,000 radians/second (1591 Hz) for the same diameters plotted in Figure 2. Attenuation values are substantially less for the new theory than for the Kelvin-Rall theory even for the 1000 micron diameter case. For Kelvin-Rall, the value of the attenuation exponent per wavelength never falls below 2. This means that the maximum amplitude of a wave after 1 wavelength of propagation is .00187 (about 1/535th) of its initial value under Kelvin-Rall for any diameter neural process. It makes little sense to talk of "wave propagation" and no sense to talk about "resonant responses" under these conditions. In contrast, according to the new theory, as much as 99.995% of unit wave amplitude may remain after a single wavelength. Under these very different conditions, notions of wave propagation and resonance do make sense.

Fig. 5 plots conduction velocity versus frequency for a 1 micron dendrite or spine neck versus frequency in the case where membrane conductance, g, is approximately zero.

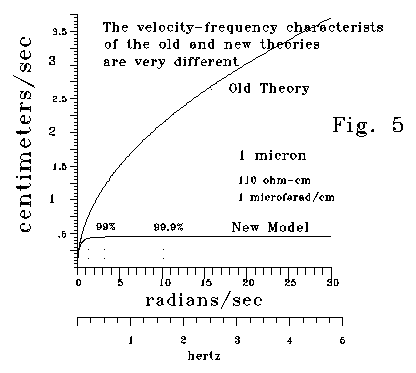
In the Kelvin-Rall theory, conduction velocity is proportional to the square root of frequency. In the S-K model, conduction velocity rapidly approaches an asymptote. Above a frequency threshold, conduction speed is almost constant. For large diameter neural processes, this threshold is so high that the velocity-frequency relation is similar for both theories. But for small neural processes, velocity is almost constant above quite low threshold frequencies. The following chart is based on a of 110 ohm-cm and a membrane capacitance of 1 microfarad/cm². For a .1 micron dendrite, 99.99% of peak velocity occurs at a very low frequency (.0511 cycles/second.)

diameter                              Frequencies for the following fractions of
(microns)                                     Peak velocity (radians/second)

                                                                  95%         99%      99.99%
  1000                                                     1,320        3,160        32,120
    100                                                         132            316         3,212
      10                                                            13.2           31.6         321.2
        1                                                               1.32           3.16        32.12
         .1                                                               .132            .316        3.212

"The 99% velocity cutoff frequency according to the new model offers a good basis for comparing phase distortion predictions between Kelvin-Rall and the new theory. Phase distortion occurs when different frequency components of a signal move at different speeds. Phase distortion can rapidly degrade the information content of a signal. In Kelvin-Rall, phase distortions are enormous. However, for the new model, in the low G limit, a dendrite or axon will have a characteristic frequency ₉₉ that has 99% of maximum propagation velocity. Above ₉₉, propagation will be almost free of phase distortion. ₉₉ correlates with diameter, conductivity, and membrane capacitance according to the relation

.

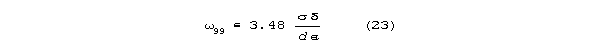The S-K theory has new, interesting characteristics in its low g, low attenuation mode. This may be described as an "on" state, in contrast to the high g, high attenuation "off" state. In the "on" condition, with g very small, important relationships are simple, particularly for small neural diameters.

Components of important formulae are the "radical value" analogous to the radius in the argand diagram characterizing the transmission line, and the angle "" on that argand diagram. The radical for the low g limit model is

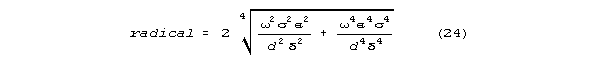
a neurally interesting characteristic emerges when this is factored as follows:

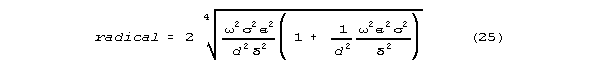
There is a term proportional to frequency (the fourth root of frequency⁴ ) The relative importance of this term grows rapidly as diameter, d, decreases. For dendrites and dendritic spines in brain, it is this frequency term that predominates. The radical can be approximated as

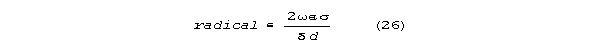
The rotational angle for the new theory is approximately

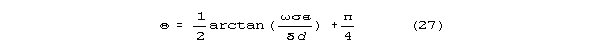
The quantity inside the arctangent above is strongly dependent on diameter scale, resistivity, and frequency.

Attenuation per unit distance is

In the range where resonance is of interest (above the 99% of maximum velocity frequency) the following approximations are useful:

For the wavelength :

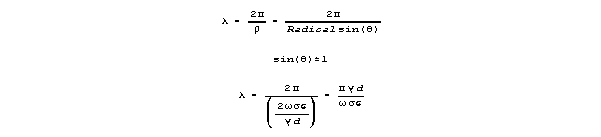
Attenuation per wavelength (in the max velocity range) is approximated as follows:

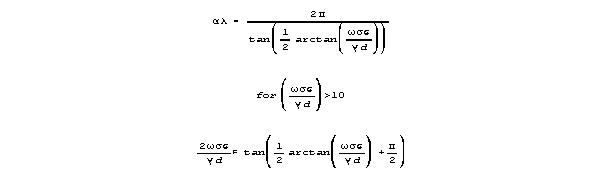
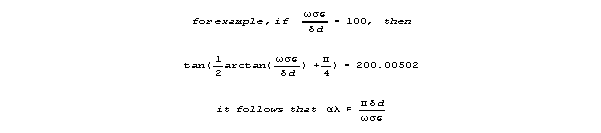
Velocity is

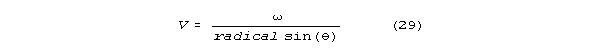
For frequencies that yeild near-maximum velocity, sin() is almost 1, and

Impedance and Impedance Mismatch Effects:

Dendritic neural passages, which function as lossy transmission lines, have impedance in the electrical engineering sense. Impedance may be defined in the usual way, but with hatted values substituted for the unhatted ones.

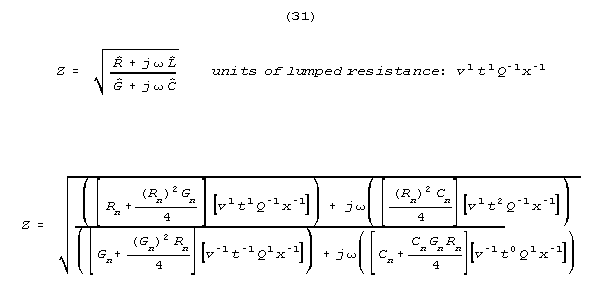
Note that impedance has the units of lumped resistance - (for the same reason that coax and other wave carrying lines are specified in ohms, with the ohmic values far in excess of the static resistances of the lines.) The interface between two sections of transmission line generates reflections unless their impedances are matched. For a line with an impedance Zo terminated in another line (or lumped resistance) called the "load", and having an impedance Z_l, the reflection coefficient Kl (the ratio of reflected to incident voltage at the load) will be

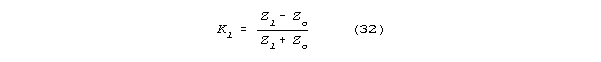
Reflection coefficient will vary from -1 to +1. When Zl>>>Z_o then K_l is approximately 1; when Z_l<<<Z_o then K_l is approximately -1; when Z_l = Z_o then K_l is 0, and there is no reflection. Similar reflection rules and similar consequences are familiar to microscopists and students of acoustics.

Impedance jumps in neural passages due to changes in crossection or g are analogous to similar sharp impedance jumps that occur in wind musical instruments. Wind instruments work because they are abruptly switchable impedance mismatch devices driven by cyclic energy input means that adapt a fluctuating input flow to match air column load. A sharply defined quasi-steady resonance is established in the musical instrument's air column. Because the reflection coefficient at the discontinuity is not perfect, some of the sound from this column radiates to listeners of the music. Analogies between the acoustical function of wind instruments and neural lines are useful when considering two linked issues.

1) A sharp change in membrane conductance, g, (whether "inhibitory" or "excitatory") can produce reflection as well as attenuation. If the change is relatively large, this reflection can be both sharp and strong.



2. Because reflecting discontinuities can be set up by synaptic or dendritic spine activity, the neural structure can operate as an abruptly switchable impedance mismatch device with variable resonance properties. This opens possibilities for logical function.

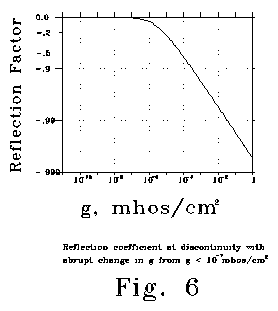
Consider a dendrite of 2 microns diameter, with a group of channels of one hundred 200 picosiemen channels over a 1 micron axial distance. Conditions are sigma=110 ohm-cm, capacitance/area=10^-6 farads/cm² ,gclosed channel=10^-12 mhos/cm². When the channels are closed, they do not effect conduction. Suppose that the channels open so that g goes from 10^-12 to some much higher value. See Fig 6, which plots a change for reflection coefficient from 1.0 to less than .0025. Fig 6 was calculated for 10 radians/second, but values for much higher or substantially lower frequencies would be about the same. Note that the difference in reflection coefficient that occurs between 10^-12 and 10^-6 mhos/cm² is small, but that very large changes in reflection coefficient are calculated for higher conductances. Opening a large number of channels in the side of a dendritic passage can change the channel from a transmission line to a sharply reflecting discontinuity. The physics is analogous to that which occurs when a clarinettist opens or covers a finger hole.

Abrupt changes in crossection are also calculated to produce analogous reflecting impedance mismatches.

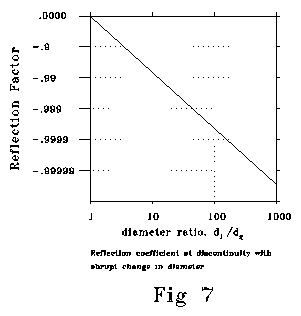
Fig 7 shows reflection coefficient at a discontinuity between a smaller and a larger diameter. Calculated conditions are sigma= 50 ohm-cm, 10^-6 farads/cm², g=10^-9, frequency=900 radians/sec, d₁=1 micron. The shape and slope of this function is insensitive to changes in frequency, initial diameter, sigma, g and c. Abrupt changes in crossection can produce strongly reflecting impedance mismatches. When changes in crossection or impedance are gradual, they can occur with little or no reflection, for reasons exactly analogous to those that permit smooth transitions in the bells of wind instruments or the gradual impedance (refraction) transitions that can be arranged in optics and in waveguide practice. The S-K equations are switching, resonance adapted equations well adapted to the information processing that brains do.

NOTES AND REFERENCES (for the annotated Koch article and Appendices):

1. Regan, D. HUMAN BRAIN ELECTROPHYSIOLOGY: Evoked Potentials and Evoked Magnetic Fields in Science and Medicine Elsevior, New York, Amsterdam, London 1989 pp 100-115.

2. Sejnowski, T.J. "The year of the dendrite" SCIENCE, v.275, 10 January 1997 pp 178

3. Appendix 2, p. 6

4. Zecevic, D. "Multiple spike-initiation zones in single neurons revealed by voltage-sensitive dyes NATURE v.381 23 May 1996

pp 322-324.

5. Regan, op. cit. Fig 1.70A and Fig 1.70B, pp 106-107.

6. The International Dictionary of Applied Mathematics D.Van Nostrand Company, Princeton, Toronto, New York, London 1960

7. op. cit.

8. C.H. Horner Plasticity of the Dendritic Spine, Progress in Neurobiology, v.41, 1993 pp. 281-231, Fig 3, p 285.

9. I believe that the extensive destruction of spines and dendrites that occurs in severe epilepsy may happen in this way.

10. I.B.Levitan and L.K.Kaczmarek THE NEURON: Cell and Molecular Biology Oxford University Press, Oxford, New York, 1991, p. 65-66.

11. When the derivation of the conduction equation from a finite "physical" model is carefully done, a series of crossterms arise in addition to the terms in R, L, G, and C. This has long been known, but the crossterms have been thought to be infinitesimal. However, when the rule that crossproducts in dimensional parameters must be evaluated in intensive (point) form is accounted for, these crossterms are finite. Crossterms that are large enough to effect neural conduction (which happen to go as the inverse cube of diameter) are included in the equation. The new crossterm parameters can be combined with the old term parameters in a hat notation. For instance, the hatted value of R includes R and a crossterm that, like R, is associated with i. The hatted value of L includes L and a crossterm that, like L, is associated with di/dt.