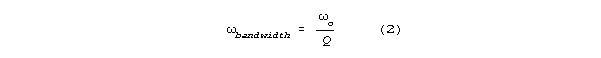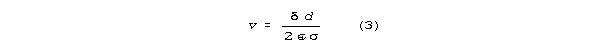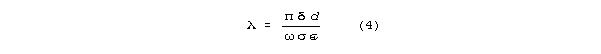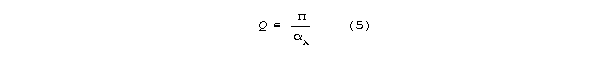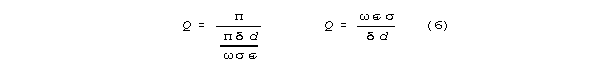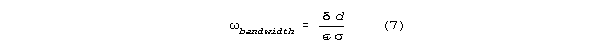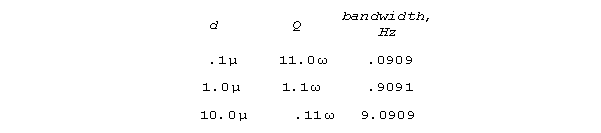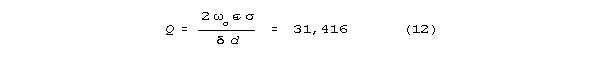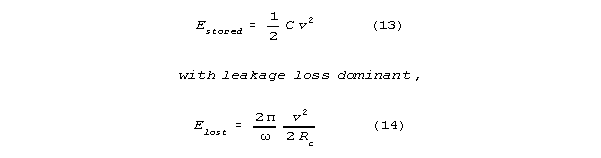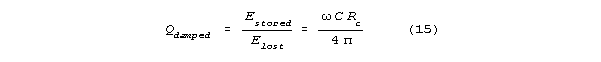The stereocilia in the auditory inner hair cells are sharply tuned resonant columns.

The dendritic spines in a channel-closed condition are sharply tuned passive resonators that may have both a LRC and a column resonant mode. Opening of one or a few channels shuts off spine resonant receptivity.

The dendritic branches, subbranches, or sections can, with spines, form resonant geometries, and these geometries may be shaped and switched by open synapses acting as impedance mismatch reflection sites.

In high g mode, spines and dendrites have very high dispersion similar to that familiar under the Kelvin-Rall (K-R) equation, and have practically no resonant properties.

        Resonance is logically interesting.    Resonant systems can effectively amplify signals of a tightly defined period and phase.   Radio and television offer familiar examples of resonant selectivity.    Radio and television receivers exist in an electromagnetic field consisting of a bewildering and undescribable variety of electromagnetic fluctuations.    Reception occurs because the resonant receiver is selective for a specific frequency at a high degree of phase coherence.    Signals off frequency are not significantly detected, and "signals" of random phase that are on frequency cancel rather than magnify in resonance.    Radar receivers also operate on the principle of resonance.   Other examples are our telephone system and cable television system, each organized so that a multiplicity of different signals can be carried in physically mixed form over the same conduits.    These "mixed" signals can be separated and detected with negligible crosstalk by resonant means.    Under the Showalter-Kline (S-K) passive neural conduction theory, dendritic spines, dendrites, and stereocilia appear to be passive resonant elements adapted to tuning and sharp on-off switching.   These are interesting characteristics for these components to have, for brains are organs of logical manipulation, and oscillations in brain are common, complicated, and known to carry information^{(2) (3) (4) (5)}.

      Under the S-K theory, brain communication occurs in TWO modes, by conduction and inductive resonant coupling, not only by conduction.    When dendritic sections or spines are in the high transmission mode of S-K, neurons not directly connected can "communicate" by inductive coupling over the extracellular medium.   Interesting possibilities follow from this. Consider the set of logical interactions that can occur among a population of people, all able to both broadcast and receive radio signals, with that population operating over many wavelengths.    The number of interactive combinations in such an interacting set is prodigious, and the coordinations possible very detailed.    Under S-K, much of the brain looks analogously adapted for sending and receiving signals in the frequency domain.    Frequency selectivity of dendritic spines and spine assemblies is high (with predicted bandwidths often less than .001 Hz and predicted Q's above 1000).    Under S-K, information flow in brain by inductive means may occur with little or no crosstalk between many frequency-defined "bands" (or multifrequency-time signatures, analogous to auditory words).    Under these conditions, the combinatorial limitation of "connectionist" neural nets (due to the explosion of N! as N increases) goes away.    Because resonant communication and processing is inherently a massively parallel process, the processing limitations of Feldman's "100 step rule⁽⁶⁾" are also much softened.    For example, resonant processing appears to be capable of handling frequency coded "list reading" functions, such as the lexical access problem, in massive parallel, without need for the very time consuming sequential search process.    (For instance, searching one word out of 50,000 might be one "resonant signal interrogation step," comprising the sending out a frequency-time signature of the word and its resonant recognition by only one tuned recieving neuron among many.)   A major reason for rejecting "symbol processing AI," in spite of its achievements and the inherent plausability of its symbol-processing approach, has been the inherent slowness and "anatomical implausibility" of the list-reading steps that AI algorithms often contain.   If neurons are capable of BOTH communication via conduction AND communication by inductive resonant coupling, as S-K and anatomy together suggest, some "theoretically impossible" animal accomplishments become less mysterious.

     Resonance-like behavior in brain has long been observed.    Evoked electroencephalographic data from human and animal subjects analyzed by David Regan's zoom fast fourier transform analysis⁽⁷⁾ shows stunningly sharp resonance-like behavior.   Most of the EEG or MEG signal power is concentrated at peaks that are exact integer multiples (or sums and differences) of evoked stimulus frequency(s).   The bandwidths of these peaks are too tight to measure, perhaps less than .002 Hz.   This tightness is astonishing when one considers that EEG must measure integrated effects over substantial volumes of brain.   If one looked at these curves from an engineering perspective, in ignorance of where they came from, one would be strongly tempted to infer an ensemble of sharply coupled very high Q passive resonators.   When the S-K equations of neural conduction are applied to anatomy, one gets an ensemble of high enough Q resonators (dendritic spines) interacting via the extracellular media, that should produce the results Regan measured.

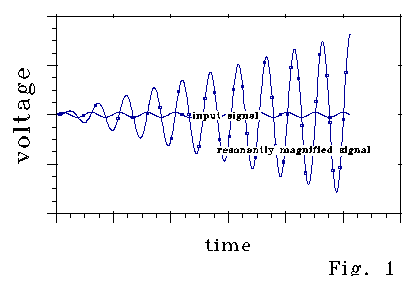
     Fig 1 shows how voltage in a passive resonator varies with input "signal" voltage.    The perturbation (input) signal is phased so that resonance builds up.   If, at some time, input signal phase shifted 180 degrees, the resonant signal would decrease at the same rate.   Around null, a shift of a few degrees makes the difference between rather rapid resonant signal increase and rapid decrease.   FM radio operates on this principle.   Phase sensitivities and frequency selectivities of such passive resonant systems are well exploited throughout communication technology.   Passive resonance seems like it may be adapted to similar sensitivities long observed in intact animals, and now seen in neurons⁽⁸⁾.

     Passive resonant systems perturbed at exactly their resonant frequency can build up energy to a value many times the amplitude of the exciting disturbance.    The steady state resonant amplification factor, Q, is an important figure of merit for passive resonant arrangements:










Bandwidth (the frequency difference between the half power points on a resonance curve) is inversely related to Q according to the formula:

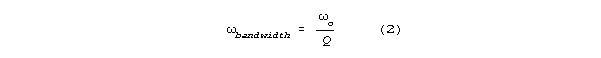
where _o is resonant frequency. Resonant systems with low damping have high Q's and tight bandwidths.


     A transmission line terminated in pure capacitance or an open or short circuit condition can have impedance properties identical to those of lumped element, and can also act as a column resonant element.   Properly terminated, a transmission line may carry waves that repeat exactly in a specific period, regardless of wave shape complexity, in the same fashion that the air column of a clarinet will carry and summate extremely complicated (but exactly periodic) waveforms⁽⁹⁾.   Such lines or columns "store" repeating wave patterns that fit the geometry of the line between reflecting ends.    They can have very high Q's.   Transmission lines of 1/4 and 1/2 wavelength have been used as resonators in the communication fields for nearly a century, and acoustically analogous columns have been used in musical instruments for millennia.   A good column resonantor would store and summate exactly periodic patterns such as those of action potential spikes, and operating in that mode on such signals could act as a very precise timing or timing comparator component.

      In engineering practice, the resonant effects produced by electrical transmission line elements tend to happen at very high frequencies ( >10⁷ Hertz).    Under neural conditions as predicted by S-K, functionally identical and strong resonant effects occur at much lower frequencies - frequencies ranging from about 1 Hz to the frequencies of bat audition, above 100,000 hz.

     A passive resonant system excited for enough cycles at its resonant frequency by a signal of RMS voltage v will build up oscillations to an RMS voltage of Q_ov.    Voltage buildup is rapid: after only five cycles of excitation, resonant voltage amplification of fifteen or more times peak voltage occurs in a high Q passive resonant circuit.



HAIR CELL STEREOCILIA AS 1/4 WAVE AND 1/2 WAVE RESONANT LINES:

     Although an enormous amount of experimental work has been done on the hair cells, the primary auditory sensors in animals, our knowledge of how hair cells work remains incomplete and tentative.   Current explanations of hair cell frequency response may be considered strained around about 400 Hz.   Bat hair cells, which, despite specializations, look much like other hair cells, function as precision navigational input instruments at frequencies more than 2000 times higher.   When the S-K equation is used, the freestanding stereocilia of the inner hair cells appear to be resonant transmission lines with the necessary resonant frequencies. The idea that stereocilia are resonant columns may be part of the explanation needed to explain the performance of real hair cells that operate at usual and high mammalian and avian frequencies.   The Regans have measured signals that appear to occur at the hair cell level, that show resonantly organized peaks consistent with column resonance in the hair cells⁽¹⁰⁾.

     Well terminated lengths of neural passage that are sharply open (short circuited) at 1/4 of wavelength L will be resonant at the frequency omega corresponding to L and at  integer multiples of omega.    An open stereocilium, or a stereocilium with an open end channel, would be an example of such a resonant structure.   A well terminated length of neural passage that is one half wavelength L, long and sharply closed on one end will also be resonant at frequency and integer multiples of omega.   A stereocilium terminated by a closed channel would be an example of such a resonant structure.   It is worth noting that the primary and overtone resonant frequencies of the open channel line are also resonant frequencies for the same stereocilium in the closed end channel configuration.

     Consider a stereocilium to be cylindrical, with diameter d cm, membrane thickness cm, membrane dielectric factor epsilon, central fluid conductance sigma ohm-cm, with a resonant frequency omega_r radians/sec and a corresponding resonant wavelength L cm.

According to S-K theory⁽¹¹⁾, the transmission velocity in the low g regime is

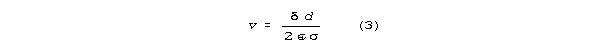
and the wavelength corresponding to frequency is

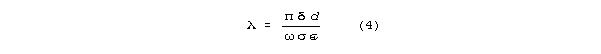
In this regime, Q>>1 and Q is inverse with attenuation per wavelength .

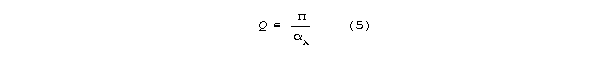
Substituting into (5) for a passage having 100% positive or negative end reflection, Q is:


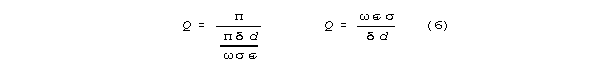
Bandwidth is

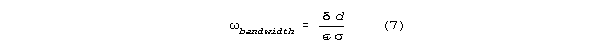
The column-resonant bandwidth for set diameter, conductance, and capacitance is independent of resonant frequency (length).

Consider model stereocilia for set   sigma = 110 ohm/cm and  
capacitance = 10^-6 farads/cm² for different diameters.

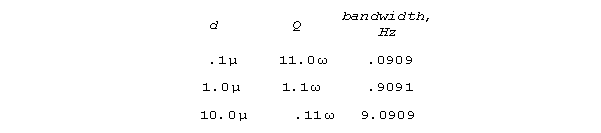
For these conditions and a resonant frequency of 1000 rads/sec (159.15 Hz) a free standing and well terminated .1 micron stereocilium will have a Q of 11,000 and a bandwidth of .0909 Hz. (A stereocilium in a bundle of other stereocilia would be more complicated.)    As a 1/4 wave line, length for this freestanding stereocilium would be 1.571 microns; as a 1/2 wave line, length would be 3.142 microns.    Lower frequencies would correspond to some combination of longer stereocilia, larger , or smaller diameter.    Higher frequencies would require increased diameter; reduced capacitance (for instance, by increasing stereocilium wall thickness, as is often observed), packing stereocilia together; smaller resistivity , or some combination. Resonant performance degrades as passages become larger. Q is proportional to resonant frequency (inverse with length). At bat frequencies, extremely high Q's, very well adapted for information processing, are predicted by this simple S-R theory.

     Measurements at these scales are not yet possible, and estimates of values are therefore speculative.    Even so, on the basis of microanatomy and chemistry it seems reasonable to expect properties adequate for strong 1/4 and 1/2 wave resonance in stereocilia at frequencies ranging from 10⁶ Hz (in bats) down to a few Hz. Q's of 10³-10⁶ would be expected with essentially perfect end reflection.    The stereocilia in inner hair cells are geometrically arranged in a fashion to maximize impedance mismatch end reflection.

     Under S-K theory, stereocilium bundling in inner hair cells would seem to be an adaptation to prevent stereocilium destruction.    Under S-K theory, a single high Q stereocilium would be a fragile and short-lived structure in an ordinary cochlea.    An input signal might easily build up to a voltage greater than the dielectric breakdown strength of the stereocilium wall, destroying the stereocilium.   An adaptively changeable stereocilium length would reduce this kind of fragility, but rather large length changes would be needed to protect single stereocilia against strong, long duration signals.   High sensitivity and stereocilium survival would therefore tend to be incompatible for single stereocilia.   (Except for stereocilia in inner hair cells adapted for a short, stereotyped duty cycle.   Bat inner hair cells, that have such duty cycles, have stereocilia "bundles" with single or a few stereocilia⁽¹²⁾ .)

      Bundling of stereocilia capable of some length change would offer a defense against such resonant destruction.   If there were two or more stereocilia connected to a single cavity, and if the stereocilia had even a small ability to change length, high sensitivity would be compatible with structural survival.   If input sound stimulus was too high, a small shift in length of one or more of the stereocilia would reduce the Q of the stereocilia assembly by destructive interference.    Length changes of 10^-3 or less would produce strong attenuation in a previously high Q system.    Assembly Q might be rapidly changed from 10⁴ to 10 (or vice versa) with such an arrangement.    Stereocilia contain contractile proteins that may be adapted and somehow controlled for this purpose.

      The inner hair cell is a complex structure in a complicated environment.    It includes ornate mechanical linkage, stereocilia end channels that open and close on the basis of mechanical stimuli and would appear to shift stereocilia between 1/4 wave and 1/2 wave mode, structurally ornate arrangements of the stereocilia, and sensitive and almost certainly temporally tuned channel and messenger kinetics in the hair cell body.    Detailed discussion of these important matters is beyond the scope of this paper.   However, the high Q characteristics of the stereocilia interpreted according to the S-K equation fit well with what we know that hair cells do.

         Resonant effects also appear likely in the stereocilia of the outer hair cells, and may be involved in their membrane tension controlling functions.

DENDRITIC SPINE RESONANCE:

      Under S-K theory, combined with the assumption that the spines can exist in an all-channel-off condition, the spines are predicted to have a very high Q passive resonant mode.    From an information processing perspective, this should be an infrequent mode, with the more common mode very much like the high dissipation mode⁽¹³⁾ widely assumed.   The high resonance mode requires that all spine channels be off, and may perhaps be easily turned off in experimental manipulation.   The resonant mode description here is no complete picture of spine function, but it is believed to be consistent with what is now known about spines.

      Fig 2⁽¹⁴⁾ shows camera lucida drawings of a neuron body and proximal dendrites of a neuron showing common spine types: thin, mushroom shaped, and stubby.    Aspect ratios and sizes of all these types vary.    A stubby type with a thinner aspect would be subject to the same logic described for a closed end stereocilia.   The "thin" type and "mushroom" type can be considered as both an LRC element and a column resonant elements.   In LRC (inductance-resistance-capacitance) mode, the bag and shaft have a lumped capacitance, and shaft inductance and resistance are considered in lumped form.   In column mode, the shaft is a column open at both ends, with a capacitive termination correction at each end.

Fig. 2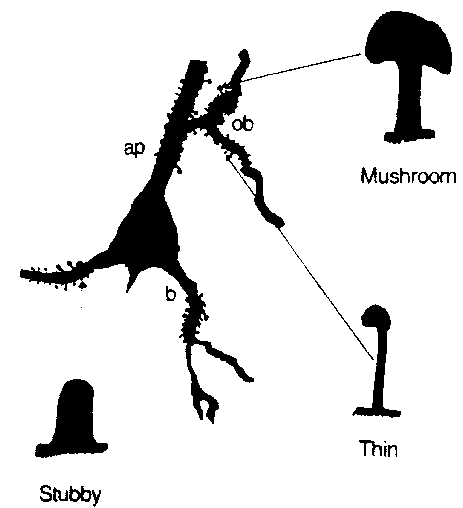

Fig. 3 shows an electrical model of a thin spine. In the scaled figure, 4/5 of spine capacitance is in the bag section.

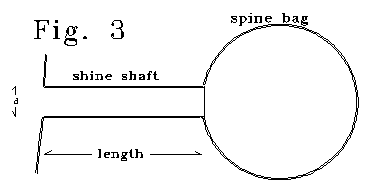
The "spine" of Fig. 3 can be modelled as an LRC resonant system. Capacitance is the capacitance of the "bag" section, plus half the capacitance of the shaft section. The shaft has resistance of R, and an effective inductance of L_ex. The L_e/R ratio is inverse with diameter. Different bag sizes for the same shaft size yield different LC products, and different resonant frequencies. Q, radian frequency, and bandwidth, for the LRC case are:

In the model, bandwidth is proportional to diameter, as in the stereocilia case.   Let's arbitrarily chose a shaft diameter of .1 µ, shaft length of .5 µ, interspine medium conductance of 110 ohm-cm, membrane capacitance of 1 microfarad/cm², and zero membrane leakage, g.   Holding these values, and varying bag size, yields the following relation between frequency and Q.

Q = _o(910) (9)

For Regan's measured frequency range of 7-45 hz (44-283 radians/sec,)   Q's between 40,000 and 257,000 are estimated.   Regan's data correspond to Q's about a decade smaller, between 3,680 and 24,000 over that same 7-45 Hz frequency range. This is an acceptable fit because:

Regan must have measured ensemble properties, not properties of single neural elements.

Regan's setup could have detected no tighter bandwidths than he did detect. and

Within the constraints of biological knowledge, we could have guessed other values of the parameters to come closer to Regan's values (or even to match them.)

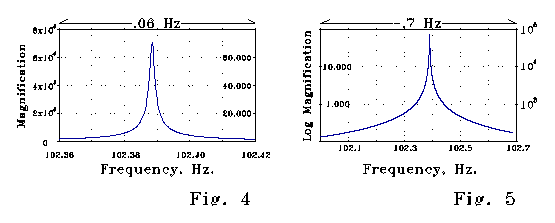
       Figs 4 and 5 below show steady-state magnification of a signal as a function of frequency calculated for the LRC spine model of Fig 3.   The peak magnification factor is about 70,000. Note the sharpness of the magnification as a function of frequency.

The model spine of Fig 3 would also have a column resonance mode.
Spine column resonant frequency will be approximately


column resonant Q from equation (6) ***** check deriv** is


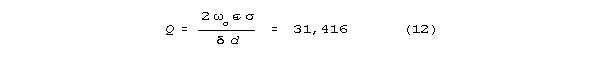
Electrical compliance of the bag would shift these resonant frequencies and Q's somewhat from the simple 1/4 wave column calculation set out above, but the correction would involve details that can be considered elsewhere.

        Referring again to Regan's data, the brain has more than 10¹³ spines.   If spine resonant frequencies are widely distributed in brain, and some fraction (say .001) of the dendritic spines are in the high Q state, one would expect long duration fixed frequency stimuli, such as Regan supplied, to yield the sort of excitation curves that Regan observed.    Coupling of the spines would be via the very rapid conduction of the extracellular medium, not via conduction along dendrites or axons.




SPINE SWITCHING:

        According to S-K, opening of one channel will change a spine from a sharply tuned state, with a Q in the thousands, to an untuned Q of 10 or less.   A single channel therefore acts to switch spine receptivity on or off.   This may be useful for neural logic, and also to eliminate resonant overload spine destruction analogous to the stereocilia destruction discussed before. (I believe that the extensive destruction of spines and dendrites that occurs in severe epilepsy⁽¹⁵⁾ may happen in this way.)    Suppose there is one membrane channel open in the bag portion of the spine.   That channel will act as a resistive, energy dissipating shunt.   The spine will have a shunt limited Q, Q_damped, that is much less than the undamped Q.   Let R_c be shunt channel resistance.    If Q_damped<<Q (which makes sense for reasonable channel conductances (between 4 and 400 picosiemens) then

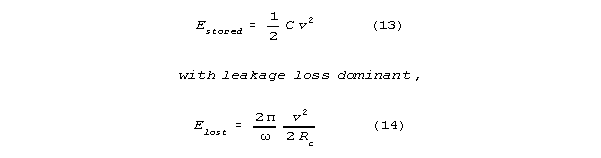
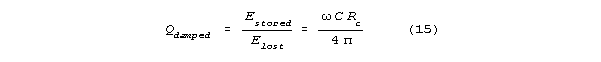
IMPEDANCE SWITCHING:

     Under S-K, dendritic conduction in the low g regime can be sharply damped, and reflected, by synapses that change local values of g quickly.    Impedance jumps in neural passages due to changes in g can act analogously to similar sharp impedance jumps that occur at pads or finger holes in woodwind musical instruments.    If the change is relatively large, this reflection can be both sharp and strong.    Reflecting discontinuities can be set up by synaptic or dendritic spine activity.    Neurons appear to be abruptly switchable impedance mismatch devices capable of switching whole dendritic trees or branches on and off.    (Such trees or branches may contain hundreds, or thousands, or even hundreds of thousands of potentially resonant spines.)


     Under S-K, one can therefore speak of dendrites, with spines, between open synapses, as more-or-less complicated "electroacoustical" resonant assemblies capable of resonating to patterns considerably more complicated (and more information-bearing) than sine waves.   My initial calculations indicate that time-frequency patterns as complicated as phonemes and simple words may be possible for anatomically plausible resonant assemblies with simple switching under S-K, and I have become interested in how such patterns might be learned, sent, and recieved by inductively coupled neuron-like systems.

        An examination of the anatomy of pyramidal cells, basket cells, chandelier cells and other neural types shows a multiplicity of axodendritic synapses at the interfaces between axons and cell bodies, and at many branch points in the dendritic arborization.   These synapses are specific to cell type and geometrically ornate. According to the S-K theory these synaptic structures would function to sharply "switch" specific portions of dendritic anatomy (which may contain thousands of spines) into or out of effective contact with the cell body and axon hillock by production of sharp impedance mismatch reflections.   This theoretical prediction is totally unproved.   However, if the prediction is true, it greatly increases the amount of information processing possible in a single neuron or small group of neurons, compared to the maximum possible under K-R.

According to the hypothesis set out here, neural function has much in common with the function of electronic communication circuits. Even so, there are pronounced differences:

The lines themselves are bistable. Conduction along neural lines occurs in two very different modes, depending on the value of g determined by channel openings.

Neural line inductance is inverse with the cube of diameter, where electronic line inductance is diameter-independent in the absence of magnetic inductance. This means that a spiny dendrite is no simple analog of an antenna, even without the complicated switching that exists according to S-K.

Neurons have huge numbers of many widely distributed and variously controlled current sources (ion channels). and

Under S-K, neurons are capable of prodigious numbers of rapidly variable switching states.


One theoretical implication of S-K theory is this: resolution of much neural function will have to be determined by experiment.    There are too many combinations to conceive of or choose from.    However, theory may sometimes be useful to identify patterns and choose among alternatives.

   When the S-K equations for passive neural conduction are substituted for the K-R equations, resonant and switching mechanisms that appear adapted to audition and neural logic follow from simple calculations combined with our knowledge of neural anatomy.  

    The S-K equations themselves follow from a conclusion that can be expressed in two ways:         
1) J.C. Maxwell's first method is the proper method for deriving complete equations from physical models⁽¹⁶⁾ or, equivalently    

2) In derivations from physical models, crosseffect terms involving dimensional parameters must be algebraically simplified in intensive form⁽¹⁷⁾.

These alternative statements of a conclusion in the theory of physical modelling are therefore of interest in neurobiology.

NOTES

1. Department of Curriculum and Instruction, School of Education, University of Wisconsin, Madison USA email: showalte@macc.wisc.edu

2. Llinas, R. Intrinsic electrical properties of nerve cells and their role in network oscillation Cold Spring Harbor Symposia on Quantitative Biology 55, 933-938 (1990).

3. Llinas, R., Ribary, U. PNAS 90 2078-81 (1993).

4. Wehr M. & Laurent, G. NATURE 384, 162-166 (1996).

5. Naatanen R. et al NATURE, 385 432-434 (1997).

6. Feldman, J.A. COGNITIVE SCIENCE 9, 1-2 (1985).

7. David Regan HUMAN BRAIN ELECTROPHYSIOLOGY: Evoked Potentials and Evoked Magnetic Fields in Science and Medicine Elsevior pp. 106-108 (1989).

8. Koch C. NATURE 385 207-210 (1997).

9. Newman, R.B SOUND, ENCYCLOPEDIA BRITANNICA 15 Figs 7, 8.

10. Regan, op. cit. pp 276-278.

11. Showalter, M.R. A New Passive Neural Equation Part a: derivation. available FTP angus.macc.wisc.edu/pub2/showalt

12. Vater M, Lenoir M. J of COMP. NEUROLOGY 318(4) 367-79 (1992).

13. Rose, G.J., Call, S.J. PNAS 89 9662-5 (1992).

14. C.H. Horner Plasticity of the Dendritic Spine, Progress in Neurobiology, v.41, 1993 pp. 281-231, Fig 3, p 285.

15. Muller, M., Gahwiler, B.H., Rietschin, L. PNAS 90 257-61 (1993).

16. Showalter, M.R. and Kline, S.J. Modeling of Physical Systems According to Maxwell's First Method. available FTP

angus.macc.wisc.edu/pub2/showalt

17. Showalter, M.R. and Kline, S.J. Equations from Coupled Finite Increment Models Must be Simplified in Intensive Form available FTP. angus.macc.wisc.edu/pub2/showalt