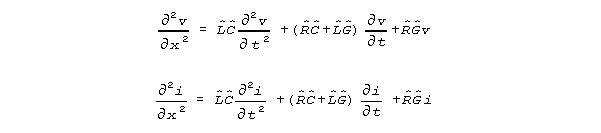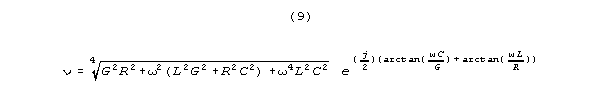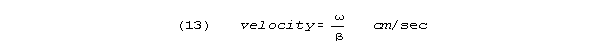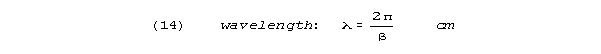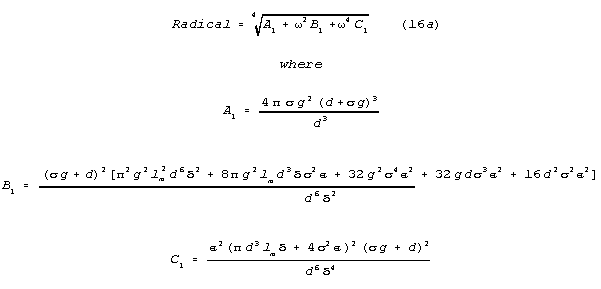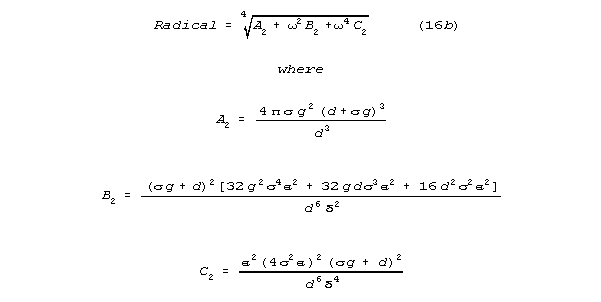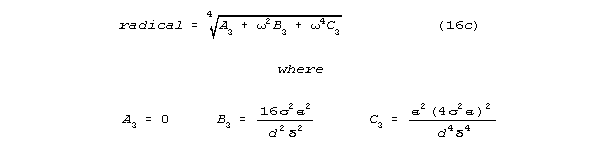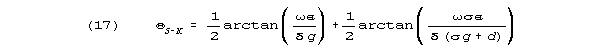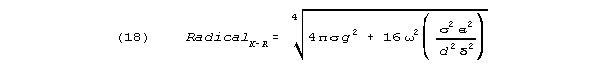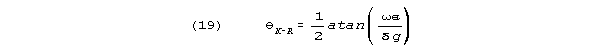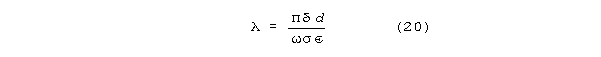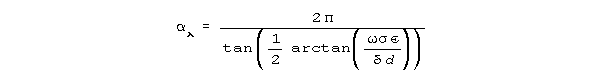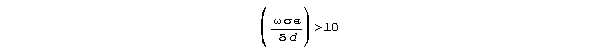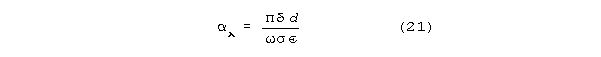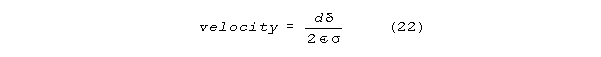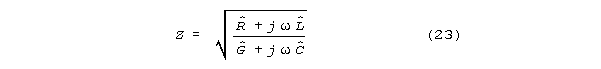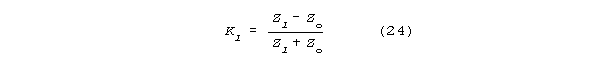A new passive neural
equation. Part a: derivation
The
now-accepted model of passive neural conduction (the Kelvin-Rall or K-R
model(2)) is based on differential equations
of conduction that lack significant terms(3)
(4). Characteristics of
a more correct set of conduction equations (that we call Showalter-Kline,
or S-K equations) are derived, discussed, and compared to the K-R equations
according to a long-established electrical engineering analysis.
For very low values of membrane conductance, g, and small diameters, the
S-K and K-R equations predict very different neural properties discussed
in detail in companion papers.
The K-R equations are the standard
conduction equations of electrical engineering, usually written in a contracted
form that discards the terms in L that are negligible compared to
R, C, and G in neural cases.

We have found that these equations lack crossterms because special restrictions
on the use of dimensional parameters in coupled finite increment equations
have not been understood2, 3. The crossterms, some of which
can also be derived (within a scale constant) by standard linear algebra
based circuit modelling (Showalter, in preparation), are negligible in
most engineering applications. But the crossterms shown here are very large
in the neural context. The S-K equations are of the same form as
the standard conduction equations of electrical engineering and are written
as follows.
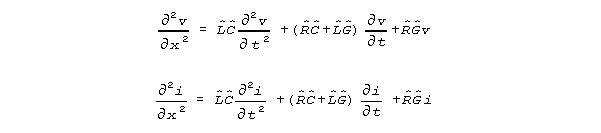
For set values of R, L, G, and C, these equations
have the standard electrical engineering solutions. The hatted values are
based on a notation adapted to crossproduct terms. In this notation, the
dimensional coefficients are divided into separate real number parts (that
carry n subscripts) and dimensional unit groups, as follows.

For wires,, the crossproduct terms are
negligible, and the two kinds of equations are the same. But
under neural conditions the crossproduct terms are LARGE.
For instance, effective inductance is more than 1012
times what we now assume it to be.
The S-K equation predicts two modes of behavior.
When G is high (some channels are open) behavior similar to that
of the K-R model is predicted.
When G is low, transmission has very low dissipation, and the system
is adapted to inductive coupling and resonance.
Under S-K, attenuation of
waves per wavelength or per unit distance varies over a much larger range
than occurs under K-R. There is a low membrane
conductance regime where attenuation of waves is small, and wave effects
are predicted. However, as channels open attenuation
increases enormously. Under S-K a neural passage
can be either sharply "on" or sharply "off" depending
on the degree of channel-controlled membrane conductance.
In the high g regime, attenuation per wavelength values are qualitatively
similar for K-R and S-K.
The standard engineering
analysis of a transmission line will be used in this paper for both K-R
and S-K, to provide direct comparisons between the predictions of these
different neural conduction models. The parabolic
equations of K-R are subsets of the usual hyperbolic equations of
conduction that occur when L=0 and the terms in L are deleted.
Setting L=0, the customary hyperbolic equations can be applied
to the K-R as well as S-K.
Transmission line analysis describes the
propagation of a fluctuating voltage (or current) source along a line in
terms of two variables, attenuation per unit distance, , and a propagation
number, , and radian frequency . These variables determine
propagation velocity, wavelength, attenuation in one wavelength, and other
values. For example, in the standard electrical engineering formality,
voltage proceeding in the positive and negative directions as a function
of distance and time is


where Vo is maximum voltage at distance zero, and
plusses and minuses denote conduction up and down the line.
In this standard electrical engineering analysis, and are
the real and imaginary parts of a complex characteristic number ,
as follows:
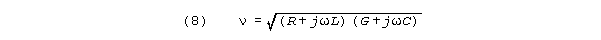
as a polar expression in the imaginary plane this is:
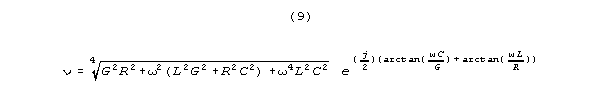
The radical part of the expression corresponds to a radius. The exponent
on e, raised to an imaginary power, corresponds to a rotation in
the imaginary plane. The quantity

is an angle in the complex plane. In K-R the range of is from
0 to 45 degrees. In S-K, the range of is from 0 to 90
degrees.
The attenuation per unit distance, is
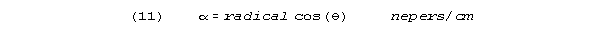
An n neper decay is a decay factor of e-n. When
approaches /2 (90 degrees) cos(), and hence attenuation,
approaches 0. Wave phenomena become important under these circumstances,
which occur in S-K but not K-R.
The wave propagation number, , is
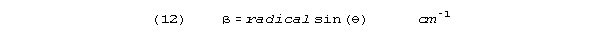
Important relations are:
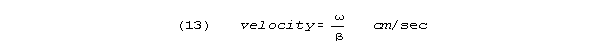
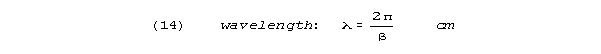
Attenuation in one wave length is
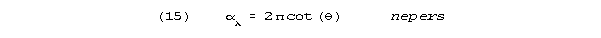
Consider a neural (dendritic) passage
in terms of its defining variables, conductor diameter, membrane
thickness, membrane dielectric constant, and axolemma conductivity,
Including electromagnetic inductance per length, lm, the radical
is:
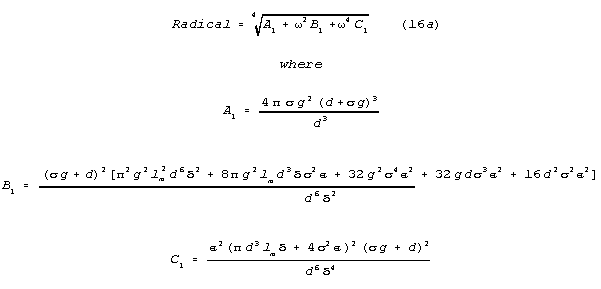
in the neural case, lm is negligible compared to the other parameters,
and is neglected. Setting lm to 0, the radical is
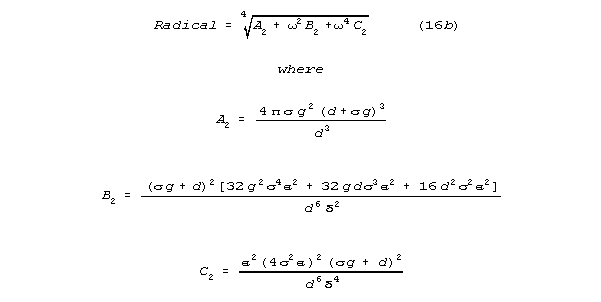
The case where membrane conductance, g, is nearly zero has special, logically
interesting properties. Setting g to 0, the radical becomes:
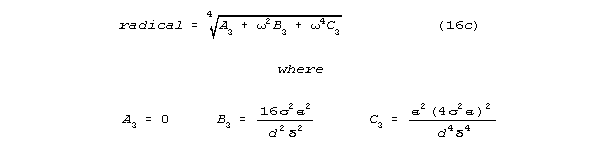
The S-K formula for angle is
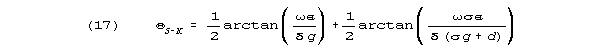
theta can approach a maximum value of /2, a value that corresponds
to 0 attenuation.
These relations are different from those of K-R, which are set
out in terms of the intensive variables below.
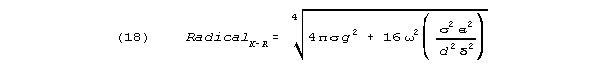
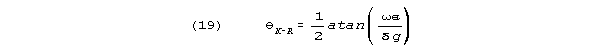
ThetaK-R approaches a maximum of /4, so that attenuation
in one wavelength is always 2 nepers or more.
CLOSE APPROXIMATIONS:
For S-K in the low g
regime, the following are very useful and quantitatively accurate simplifications.
For wavelength:

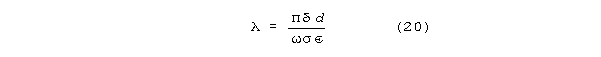
For attenuation per wavelength:
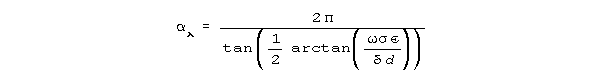
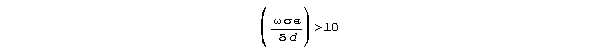
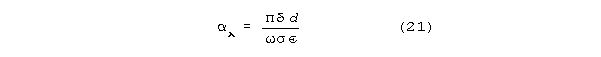
When the fourth root C3 term in (16c) dominates
the radical, conduction velocity becomes independent of frequency(5),
and simplifies to
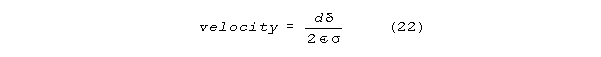
IMPEDENCE EFFECTS:
Dendritic neural passages will have impedance
in the electrical engineering sense. The standard models
for reflection at impedance mismatches that apply in electrical transmission
lines also apply to neural transmission under S-K.
Impedance may be defined in the usual way, but with hatted values substituted
for the unhatted ones.
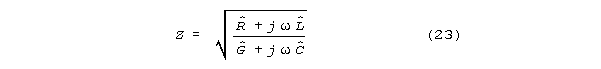
Impedance has the units of lumped resistance,
as in coax and other wave carrying lines. The interface
between two sections of transmission line will generate reflections unless
their impedances are matched. For a line with an impedance
Zo terminated in another line (or lumped resistance) called the "load",
and having an impedance Zl, the reflection coefficient
Kl (the ratio of reflected to incident voltage at the load) will be
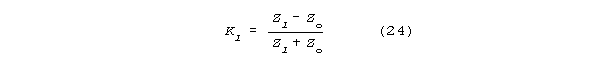
`Reflection coefficient
will vary from -1 to +1. When Zl>>>Zo
then Kl is approximately 1; when Zl<<<Zo
then Kl is approximately -1; when Zl
= Zo then Kl is 0, and there is no
reflection. Similar reflection rules are familiar
in optics and acoustics.
NOTES:
1. Department of Curriculum and Instruction, School
of Education, University of Wisconsin, Madison Wi. USA email: showalte@macc.wisc.edu
2. Rall, W. "Core conductor theory and cable
properties of neurons" HANDBOOK OF PHYSIOLOGY - THE NERVOUS
SYSTEM V.1 Ch. 3 Williams and Wilkens, Baltimore, Md. (1977).
3. Showalter, M.R and Kline, S.J. Modeling of
Physical Systems according to Maxwell's First Method available FTP
and on
the web
4. Showalter, M.R. and Kline, S.J. Equations from
Coupled Finite Increment Physical Models Must be Simplified in Intensive
Form available FTP
and on
the web
5. Showalter, M.R. A New Passive Neural Equation.
Part a: derivation Fig. 4. available FTP angus.macc.wisc.edu/pub2/showalt