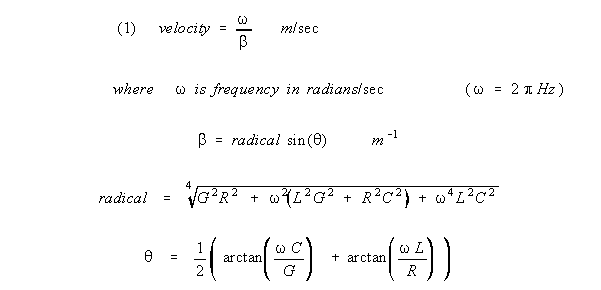
Conduction velocity - SK theory - with and without glia.

Conduction velocity in a transmission line is a function of the effective R, L, G, C, and radian frequency of that line (hatted values under S-K theory, unhatted values under K-R theory.)     See A new passive neural equation: Part a, derivation             Equation 1 below is equation (13) in this reference.     Equation 13 was written in CGS units, but it has been found that units of M-K-S are required for correct statement of the crossterms in the S-K theory.

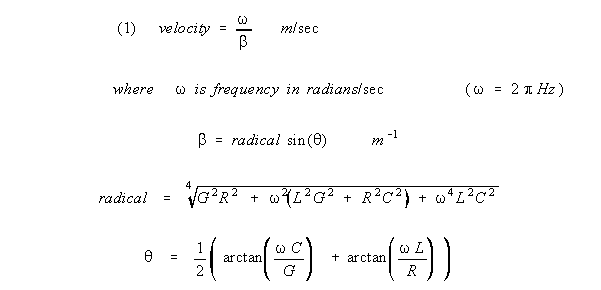
Writing (1) out, velocity is:

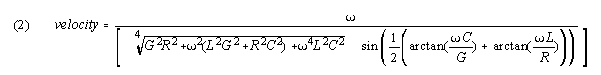
For the S-K case, the relevant values are the hatted values that include crossterms, and effective inductance is large, rather than negligible.    The hatted values are based on a notation adapted to crossproduct terms. In this notation, the dimensional coefficients are divided into separate real number parts (that carry n subscripts) and dimensional unit groups, as follows.

     


For S-K theory, hatted values replace unhatted ones, and equation (2) becomes:

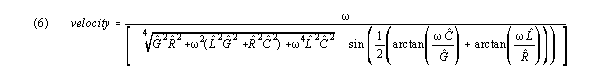
In the case where G is negligible, G hat is negligible and (6) reduces to

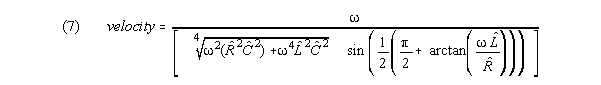
For small neural lines under S-K theory, the numerical value of Lhat is much larger than Rhat.    (This contrasts with K-R theory, which corresponds to the unhatted values of R, L, G, and C, under conditions where L, electromagnetic inductance, is negligible. )     Under S-K theory the RhatChat term is only important at very low frequencies.    As frequency increases, the LhatChat term dominates and the velocity function gets closer and closer to

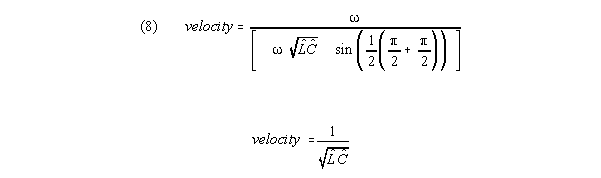
So under S-K theory, velocity for small neural lines, with G very low, is INDEPENDENT of frequency, because frequency effects in numerator and denominator cancel.    

Velocity is also substantially lower than the velocity based on the Kelvin-Rall theory, where Lhat ~ 0 .

Let's calculate this velocity in terms of its parts, which are functions of capacitance per unit membrane area and axolemma resistivity. We'll use subscripts to show that we are dealing with the real number parts of these values (in the MKS unit system). ( Under neural conditions, L, the electromagnetic inductance, is a negligibly small part of Lhat, and is ignored below. )

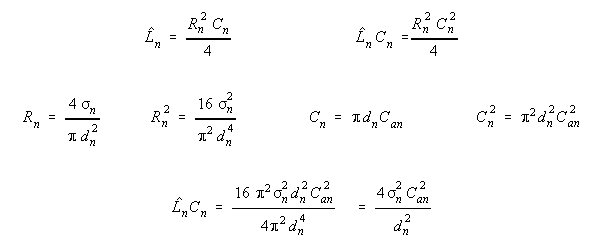
In the limit where the LC term is dominant, velocity is calculated simply.

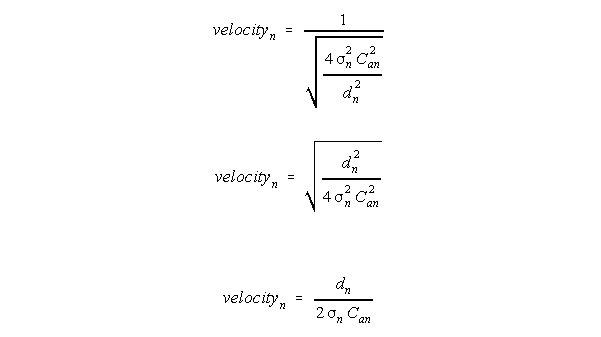
This is a simple formula, with a numerical value that corresponds to meters/sec. Velocity is directly proportional to line diameter, and inversely proportional to resistivity and capacitance per membrane area. In the case of unmyelinated neural lines without glia, the formula yields very low predicted velocities. The following values of C_a and resistivity are in commonly accepted ranges.



For an 2 micron line with these values, conduction velocity is .0002 meter/sec (.02 cm/sec.) For low values of G, that velocity would be independent of frequency - the same for 10 Hz or 10,000 Hz.

                    (Different values of resistivity and membrane capacitance could be chosen - but all                      reasonable values would correspond to low velocitities in the glia-free, unmyelinated                      neural line case.)

The Kelvin-Rall theory  predicts much higher velocities, and velocities that vary as the square root of frequency.   The table below compares predictions of the K-R and S-K theory, for the same 2 micron low G line:

                                          KR velocity      SK velocity               KR/SK

                  1 Hz                 .042 m/sec        .0002 m/sec             210 : 1
              100 Hz                 .42 m/sec          .0002 m/sec            2100 : 1
         10,000 Hz                  4.2 m/sec          .0002 m/sec          21000 : 1

GLIA:

The S-K theory velocities above are very low, but also apply to an artificial case.   Neural lines in vertebrate brains are never, or practically never, seen without a glial surround. Reasons for that consistent glial surround have been long discussed, but remain unclear in the literature.   S-K theory offers a reason for the glial clefts. Under S-K theory, the cleft between neural membrane and glial membrane results is about a 100-fold reduction in effective capacitance per unit membrane area under the dynamic conditions that apply to neurons, and about the same 100-fold factor of reduction in energy consumption per A.P. http://www.wisc.edu/rshowalt/cleft .   S-K theory conduction velocities, with glial surround, are about 100 times higher than those shown above.  

(The effect of glia under K-R theory is harder to calculate, and much less than in S-K theory.)